MagnificoChen.github.io

第一章 简介

术语计算机图形学描述的是使用计算机创作或进行修改图像的所有功能。这本书介绍了数学和算法工具，可用来创造各种图像——拟真视觉效果、包含大量信息的插图，亦或是好看的计算机动画。图形可以是二维或者是三维的；图片可以是完全合成的或者是对原有照片修改得出的。此书主要讲的是基础的算法和数学原理，主要涉及对三维的物体和场景进行渲染，得出图像。 实际上，研究计算机图形学会不可避免的需要一些关于硬件、文件格式、一两个图形 API 的知识储备。计算机图形学是一个快速发展的领域，所以这些领域的的专业知识一直处于发展之中。因此，本书中，我们将避免使用特定的一种硬件或 API 的造成的局限性。我们建议读者根据现有的软硬件技术来自行补充书中的知识。幸运的是，计算机图形学的发展史已经足够形成一套概念体系，本书中讨论的知识和概念将在大多数环境中都可用。 本章定义了一些基本的术语，提供了一些关于计算机图形学的信息源和发展的历史背景。

1.1 图形学的领域

给一个领域强加应用场景是不合适的。但大多数从业者都会同意下面这几个方面是计算机图形学的主要应用领域：

还有其他领域也包含了计算机图形学的相关技术。但计算机图形学是不是其关键技术还有待商榷。这些领域将如下所述：

1.2 主要应用场景

几乎所有地方或多或少都可以用到计算机图形学，但计算机图形学的真正客户还是以下的工业场景：

1.3 一些图形 API

使用图形库的关键是会使用图形 API。API 是一个用来完成相应功能的基础函数集，而图形 API 则指的是一些关于图形基本操作的函数集合，如渲染图像和 3D 表面到屏幕上的操作。

所有图形界面的程序都需要用到两个相关的 API：用于视觉效果输出的图形 API 和用于获取用户输入的 UI-API。首先，人们进行了集成的探索，如 Java，图形和 UI 工具是集成在 Java 中是它的一部分，且可移植、被完全支持。第二次探索以 Direct3D 和 OpenGL 为代表，渲染指令和 C++一样，是软件库的一部分，UI 界面则是另一个独立的实体，不同系统可能显示的不一样。在后者的探索中，编写可移植的代码较为困难，尽管编写小程序可以使用可移植库层来封装特定的系统 UI。

不管您选择什么 API，基本的图形调用指令大多都是一样的，这些正是本书讲述的内容。

1.4 图形流水线

现在所有的 PC 都有一个强劲的 3D 图形流水线。图形流水线是一个特殊的软硬件子系统，用来绘制 3D 图元。通常来说这些系统对处理有共点的三角形有特殊优化。流水线的基本操作内容是：将 3D 的顶点映射到 2D 平面，然后将三角形加上阴影，这样他们就能看上去和真的一样，并且处在正确的前后关系中。

虽然将三角形绘制出正确的前后关系曾经是计算机图形学的最主要研究方向，现在这个问题一般使用 z-buffer 算法解决。z-buffer 算法通过使用一个特殊的缓冲区来进行暴力计算。

事实证明在图形流水线中进行的几何运算也基本可以在 4D 空间内通过 3D 坐标加上一个相同的坐标来表示，以此帮助透视投影。这些 4D 坐标空间由 4x4 矩阵和 4 维向量组成。因此，图形流水线配备了大量的处理这些矩阵和向量的硬件结构。这套 4D 坐标系统是计算机科学中最漂亮的结构之一，也是学习计算机图形学时需要越过的最大难关。每本图形学书籍的第一个部分都是在讲解这个部分。

图片的生成速度取决于有多少个三角形需要绘制。因为在多数程序中，互动性远比视觉质量重要，所以需要将每个模型的所需三角形尽可能的降到最低。并且，如果这个模型比较远，那么就不需要那么多的三角形来描述它。使用 LOD（多级细节描述）来描述一个模型是很有用的。

1.5 数值问题

很多图形程序仅仅只是由处理 3D 数值的代码构成的。数值问题是这些程序中起决定性作用的一环。在以前，由于机器表示数据的方式不同，将该问题解决得既可移植又稳定简直是天方夜谭。更糟糕的是机器处理异常的方式不一样且不相互兼容。幸运的是，几乎所有计算机都遵循 IEEE 浮点数标准，这让程序员得以更方便的设定什么情况该对数值进行怎样的操作。

尽管 IEEE 浮点数在进行数值计算时很有用，我们在图形学研究时遇到的情况只有那么几个。第一、也是最重要的，是 IEEE 浮点数有三种特殊值：

  1. 正无穷(∞) 这是有效数值中最大的数值。
  2. 负无穷(−∞) 这是有效数值中最小的数值。
  3. 非数值(NaN) 这不是数值。通常由于未定义的行为（如 0 除以 0）产生。

IEEE 浮点数的设计者做了一些定义，所以程序员用起来非常方便。其中大部分规定是上面三种数值进行运算的结果规定，某些时候这样做会产生异常，但很多时候这些错误是可以不管的。特殊地，我们制定了一个正实数 a，下面的规则对应了 a 除无穷的情况：

其他包括无穷值的运算和你想得差不多。还是以 a 为例：

下列判断也和你想的差不多：

包括 NaN 的表达式比较简单：

可能这里头最有用的就是除 0 如何定义了。同样以 a 举例，下面是相关规定：

很多计算在使用 IEEE 规则时会变得非常简单。比如：考虑以下算式：

\[a=\frac{1}{\frac{1}{b}+\frac{1}{c}}\]

这种算式会在计算电阻或焦距中遇到。如果程序因为除零错炸了（以前不用 IEEE 浮点数的计算机就会这样）,然后就需要两个 if 语句来检查 b 和 c 是否为无穷小或 0。而使用 IEEE 浮点数后，如果 b 或 c 是 0，那么 a 算出来就是 0。另外一个好用之处在检查 NaN 时不需要麻烦的步骤了：

\[a=f(x)\\ \rm\textbf{if}\ (a>0)\ \textbf{then}\\ \rm{do\ something}\]

上面这段程序的 if 条件并没有完全覆盖，因为 a 有可能是无穷或 NaN。但由于我们定义了那些情况，所以省去了额外的判断，这能让程序更健壮、效率更高。

1.6 代码效率

世界上没有能让代码更高效的免费午餐。代码效率需要通过谨慎的权衡来实现，而不同架构的权衡方法不一样。虽然但是，我们在今后更应该将注意力放在优化访存效率，而不是将重点放在优化操作次数上。出现这个变化的原因是内存技术的发展没有跟上处理器的发展速度。而且，出现了这个变化后，利用内存的局部性原理来进行内存访问的优化更显重要。

一种可行的提高代码速度的方法如下，您可以寻找需要的步骤来自行处理：

  1. 尽量保持代码的简洁易懂。尽量在运算结束后就输出数据，而不是存在某个地方。
  2. 在优化模式下编译。
  3. 使用分析工具来找出代码的瓶颈。
  4. 检查用到的数据结构来增加数据的局部性。如果可以的话，让数据大小和目标硬件上的 cache/page 大小一致。
  5. 如果分析工具发现了数值计算方面的瓶颈，那么可以检查以下编译出来的汇编语言看那个地方有低效的环节，最后重写代码解决问题。

最重要的步骤是第一步。大多数所谓“优化”会让代码变得更难读，但速度也变不了多快。而且，相比日后对难懂的代码进行 debug，将这些时间用于优化其他的地方显然更值。除此之外，您还需要小心那些老掉牙的建议。以前优化的典中典操作是将实数类型改成整数类型，但现在的 CPU 算这俩已经一样快了。但不管怎样，优化后需要进行性能分析来确保你确实是在各种环境下都进行了优化。

1.7 设计和编写图形程序

编写图形程序时，有一些技巧可以通用。这一节我们为你提供了一些建议，可以在实现图形程序时对你有帮助。

1.7.1 类型设计

“我认为 KISS（保持简单、保持愚蠢）的原则很有用。弄两个类型出来我觉得和它带来的复杂度相比不划算。 –作者 1

我喜欢将点和向量分开，这让代码更易读，也方便编译器找 bug。 –作者 2

设计图形程序的一个关键点就是：图形程序要有良好的类或架构设计提供给几何体，如向量和矩阵。这种设计也可以用于 RGB 颜色或图像上。设计的结构应尽可能的简单高效。一个广泛讨论的问题就是位置坐标和位移变换是否应该分由两个不同的类进行管理。如：一个位置变量自乘 1.5 倍是没有意义的，但位移就会有意义。这个话题很难达成共识，所以下面的例子将不会管这么多，我们会将两者视作统一。

所以，一些基本的类可以如下定义：

另外，你可能想要添加一些类，他们是区间、正交基、坐标系框架。

你可能会想要单独为单位向量开一个类，但我发现这样不值当。 –作者 1

1.7.2 单精度与双精度浮点型

对现代的设计体系来说，要保证代码高效率，关键就是要将内存使用率降低，以及保持内存的连续性，照这样说的话，应该建议使用单精度浮点型。然而，为了避免数值计算发生的精度问题，双精度浮点型又更加适合。这两者的权衡由具体程序而定，但在你的定义里指定一个默认情况会更好。

我的建议是在集合计算时使用双精度，在颜色计算时使用单精度。针对那些很占内存的东西，如三角网格，我建议使用单精度，但数据通过成员函数时应该转化为双精度。

1.7.3 对图形程序进行 Debug

如果你问身边的人，你就会发现越是大佬，他们就越少用传统的 debug 工具。其中一个原因是对于复杂程序来说，再用这种工具会比小程序麻烦的多，然后还有一个原因是最深藏不露的 bug 往往是由于某些概念被错误地实现了，然后你就会在找变量过值上浪费大量时间。我们找到了一些图形编程中挺不错的 debug 技巧。

科学的方法

在图形编程中，有一个相比与传统调试更有用的方法。只不过，当你是菜鸟时，别人会和你说不要这样做，所以你使用这个方法的时候有点理不直气不壮：我们创建一个图像，然后观察它出了什么问题。然后我们猜是不是由于某某原因造成，测试这个假设。比如，在一个光线追踪项目中，我们可能会发现有很多不知道为啥很暗的色块；这就是我们初学光线追踪经常遇到的问题，叫“shadow acne”。而在这个项目中，传统的调试方法不管用。与之相对，我们需要意识到阴影线射在暗处的表面，然后可能会注意到那些暗处的颜色就是环境色，所以做出判断：是直射光缺失了。而直射光是会在阴影部分被关闭的，所以可以做出这样的假设：那些地方被错误地设置为阴影，所以他们照不到光。为了验证这一假设，我们可以先关闭阴影选项重新进行编译，这样可以判断是否因为错误设置阴影导致的错误；然后继续探究问题。这个方法有时候非常管用的原因是：有时候我们不一定非要找到错值和错误概念，相反，我们可以通过试验来缩小范围。基本上试几次就能够找到原因，这样的 debug 过程是令人快乐的。

将图片作为 Debug 的输出

很多时候，得到一个图形程序的调试信息的最简单方式就是输出图像它自身。如果你只需要一部分运算结果，但运算是针对整个图像，那么你可以将这个值直接放到输出图像上，然后跳过后续计算，直接输出原图像的那个小部分。打个比方：如果你怀疑是由于表面法线导致阴影计算出错，你就可以将正确的法向量直接放到图像上去，这样输出的结果就是用你正确的法向量计算出来的结果。或者，如果你怀疑某个特定值有时候超范围，那就可以通过往超范围的像素改成红色的办法找到错误位置。其他的好办法，如将应该不可见的地方涂上显眼的颜色标记、使用物体的 ID 标记图像、或是以不同的颜色区分像素计算的任务轻或重等。

使用调试器

真香。因为还有一些案例是上面两种方法都没法判别的。主要麻烦的地方是图形程序经常会运行很多次同样的代码（比如每个像素/每个三角形执行一次），这会让一步一步的调试方法变得不切实际，而且很多烦人的 bug 经常在复杂输入的情况下发生。

一个有用的方法是给 bug 设置一个“陷阱”。首先，保证你的程序是准确的-在单线程中运行，从固定种子中取数计算；然后，找到哪个三角形或像素有问题，然后在那个地方加上一些代码，让他在出错时才会执行。如，如果你发现位于（126，247）位置上的像素看起来有问题，那么你可以加这一句代码：

\[\rm\textbf{if}\ (x=126\ and\ y=247)\ \textbf{then}\ \\ \rm{print(blarg!)}\]

如果你在 print 语句上设置一个断点，那么在你关心的那个像素计算时你就会进入调试模式。同时有些调试器可以不需要你添加代码也能达到同样效果，称作“条件断点”。

在程序崩溃的情况下，调试器还是很有用的。你可以回溯程序，使用断言，然后重新编译，来找到程序哪里出了问题。而这些断言可以留在程序里，以防你之后又写了什么一样的 bug 出来。这同样说明了传统调试模式的弊端，因为传统调试模式没法让你往程序里加新的有用的断言。

调试中的数据可视化

通常你是很难理解你写的程序究竟做了什么，因为它在报错之前已经计算了一大堆中间结果了。这种情况就和测量特别多数据的科学实验比较类似，所以也有一个相同的解决方案：将数据绘制成易懂的图形。比如，在光线追踪中，你可能会将光线束可视化，这样你就能看到有哪些通道构成了这个像素，或者在重新采样图像时，你可以将所有点绘制成一幅图，来显示通过输入进行采样的结果。你花在数据可视化上的时间会带来回报，可以使代码变得易读，优化时变得简单。

我喜欢格式化的 debug 输出，因为这样输出利于绘图，能帮助我调试程序。 –作者 2

后记

这里关于软件工程方面的讨论受到了《Effective C++》系列书籍、《Extreme Programming movement》以及《The Practice of Programming》的影响。这里讨论的这些调试经验是建立在跟 Steve Parker 的相关讨论的基础之上的。

每一年都有很多跟图形学相关的会议，这就包括了 ACM SIGGRAPH 以及 SIGGRAPH Asia，Graphics Interface，the Game Developers Conference（GDC），Eurographics，Pacific Graphics，High Performance Graphics，the Eurographics Symposium on Rendering，以及 IEEE VisWeek。你现在就可以通过这些会议的名字在网上找到它们的相关资料。

第二章 数学知识补充

很多图形程序只是单纯的将数学知识翻译成代码。所以数学公式越简单，最终的代码就会越简单。所以本书致力于用正确的数学公式完成图形任务。这一章介绍了从高中数学到大学数学的各种数学工具，且排版偏向于供参考而不是供学习。这属实有点像大杂烩。每个知识点都和数学课程上学的知识点不太一样，因为这里的数学是为图形学服务的，同时为了你能看得懂书中的数学标记，这章也会讲到一些平时数学课被跳过的内容，如三角形的重心坐标。这章不打算提供大量的证明素材，而是通过几何图形来进行直观的展示和讲解。对线性代数的讲解会推迟到第五章处，因为第五章才开始讨论图形的变换。我们鼓励读者先通过本章内容熟悉概念，然后在后面遇到问题的时候可以回过头来参考。章节的课后习题可以帮助你规划复习进度。

2.1 集合与映射

映射 ，又称 函数，是编程和数学领域的基础知识。就和编程中的函数相似，一个映射接受一种 类型 的参数，并把它对应成一种类型的另一个对象。在编程领域我们一般说“类型”，这话翻译到数学领域就是 集合 。如果一个对象是一个集合中的一员，我们用 $\in$ 符号表示。如：

\[a\in S,\]

读作 $a$ 属于 $S$ 这个集合。若有 $A$ 、 $B$ 两个不同集合，我们可以通过笛卡尔积的方式算出第三个集合，用 $A\times B$ 表示。这个 $A\times B$ 集合由所有 $(a，b)$ 的组合构成，其中 $a\in A$ ， $b\in B$ 。我们同时可以使用 $A^2$ 来表示 $A\times A$ 。同样的，我们可以将此操作推广到任意维度，如三个集合，四个集合等等。

我们通常使用的集合包括：

注意 $\mathbb{S}^2$ 虽然是由三维空间的点组成的，但是他们是在球面上，可以转化成由两个参数表示，所以可以看作是二维集合。映射的标记使用一个箭头符号和一个冒号，如下：

\[f:\mathbb{R}\to\mathbb{Z},\]

可以读作：函数 f 接受实数输入，并把他映射成整数输出。在这里，箭头左边的集合称作 定义域 ，右边的集合称作 值域 。程序员可能对下面这种说法更熟悉：函数 $f$ 接收一个实数参数，返回一个整数。所以，下面两种描述是等价的：

\[\rm {integer}\ f(\rm{real}) \gets \rm{eq.} \to f:\mathbb{R}\to\mathbb{Z}.\]

所以这种冒号箭头的表达方式可以看作一种编程语法。就这么简单。

图 2-1

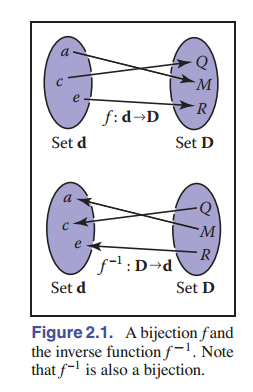
点 $f(a)$ 称为 $a$ 的 像 ，而一个集合 $A$（也就是定义域的子集）的“像”就是函数值域的一个子集。所有定义域构成的像就是值域。

2.1.1 逆映射

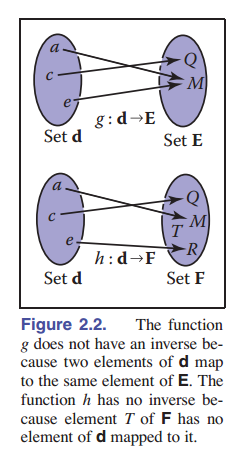
如果我们有一个函数 $f:A\to B$ ,那么就可能存在一个 反函数 : $f^{-1}:B\to A$ ，仅在所有的 $b\in B$ 都是值域中的一个点，而且此点唯一对应（也就是每个 $a$ 只对应一个 $b$ ）时，取逆操作成立。这样的映射称作 双射 。一个双射中，每一个 $a$ 都对应一个唯一的 $b$ ，而且对于每一个 $b$ 都有一个 $a$ 与之对应。不是双射的映射当然就没有逆映射这个概念。

一个双射的例子就是：在 $f:\mathbb{R}\to\mathbb{R}$ 上，规则是 $f(x)=x^3$ 。那么，它的反函数就是 $f^{-1}(x)=\sqrt[3]{x}$ 。这种表述方式不太好，因为我们发现等式两端有两个 $x$ ，所以，我们将其中一个换成 $y$ ，可以得到 $y=f(x)$ 和 $x=f^{-1}(y)$ ，更直观的可以写成 $y=x^3$ 和 $x=\sqrt[3]{x}$ 。而另外一个没有反射的是在 $f:\mathbb{R}\to\mathbb{R}$ 上，规则是 $f(x)=x^2$ 。为什么？有两个原因：第一， $x^2={(-x)}^2$ ，第二，值域的负数区域没有定义域内的 $x$ 相对应。不过，我们可以将定义域限制在 $f:\mathbb{R}^+$ ，这样 $\sqrt{x}$ 就是一个正确的反函数了。

图 2-2 图 2-3

2.1.2 区间

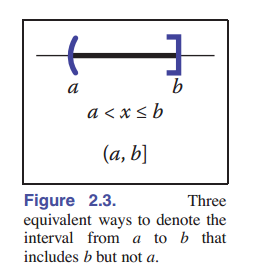
我们大多数情况会希望一个函数的定义域限制在某些值之间，由此引入 区间 的概念。区间有开闭，开区间不包括边界值，闭区间包括边界值。开闭可以在两头混用。只要我们使用了 $[a,b]$ 这样的区间，我们默认 $b$ 比 $a$ 大。最后，可以使用区间表示笛卡尔积产生的坐标。如 $x$ 是三维单位立方体中的一个点，我们可以写作 $\mathbf{x} \in[0,1]^3$ 。

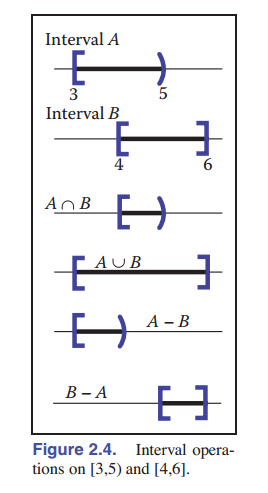
区间在与集合操作（ 交 、 并 和 差 运算）结合时特别有用。例如，两个区间的交集是它们共有的点的集合。符号 $\cap$ 表示交集。例如， $[3,5) \cap [4,6] = [4,5]$ 。对于并集，符号 $\cup$ 用于表示任意区间中的点。例如: $[3,5) \cup [4,6]=[3,6]$ 。与前两个操作符不同，差 运算符没有可交换性，不同的运算顺序会产生不同的结果。

差 运算符用负号表示。计算结果是左边区间中的、不在右边区间中的点。例如, $[3,5)−(4,6)=(3,4)$ 和 $(4,6)−(3,5)=(5,6)$ 。我们可以画一个区间图，如 [图 2.4] ，将其可视化便于理解。

区间在集合运算中显得尤为重要。区间运算有 交、并、差 等。由于此为高中内容，此处不再赘述。

图 2-4

2.1.3 对数运算

虽然在计算器出现之后，对数的作用变小了一些，但如果一个方程中出现指数项，对数还是很有用的。根据定义，每个对数项都有一个底数，用 $a$ 表示。关于 $x$ 的“以 $a$ 为底的对数”写成 $\log_ax$，定义为“a 的右上角指数必须被提高到这个数，才能得出 $x$ 的结果”，即：

\[y = \log_ax \Leftrightarrow a^y = x\]

注意以 $a$ 为底的对数和以 $a$ 为次幂的函数是互为反函数。这个定义引出下面几个推论：

\(a^{\log_a(x)} = x;\) \(\log_a(a^x) = x;\) \(\log _a (xy) = \log_a x +\log_a y;\) \(\log _a (x/y) = \log_a x -\log_a y;\) \(a^{\log_a(x)} = \log_ab \cdot \log_bx;\)

当我们将微积分应用于对数时，会发现经常出现一个特殊数 $e = 2.718…$ 。以 $e$ 为底的对数称为 自然对数 。我们采用常见的简写 $\ln$ 来表示它：

\[\ln x \equiv \log_e x\]

注意，“ $≡$ ”符号可以读作“根据定义等价于”。像 $π$ 一样， $e$ 这个特殊的数字在很多情况下都会出现。除 $e$ 之外，许多领域还使用的特定底数进行对数运算，并在其符号中省略了底数，即 $\log x$ 。例如，天文学家通常使用 $10$ 为基数，理论计算机科学家通常使用 $2$ 为基数。由于计算机图形学是一门包含许多领域的技术，我们将避免这种简写。

我们将对数和指数求导，能发现自然对数是“自然的”原因：

\(\frac{d}{dx} \log _a x = \frac{1}{x \ln a};\) \(\frac{d}{dx} a^x = a^x \ln a;\)

我们发现上面的求导都会有一个系数，如 $\ln a$ 和 $\frac{1}{\ln a}$ 。但是如果底数是 $e$ ，这个系数就是 $1$ 。

2.2 解二次方程

一个 二次方程 可以被表示成这样的形式：

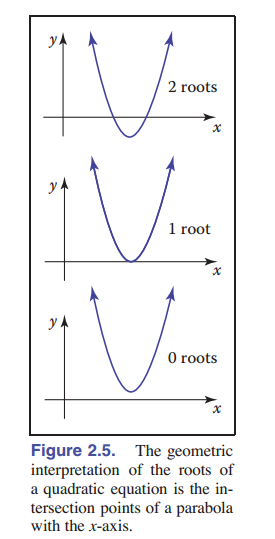
\[Ax^2+Bx+C = 0\]

这里 $x$ 是一个实未知数。$A$ $B$ $C$ 都是常数。如果在纸上画出一个二维 $xy$ 图 $y = Ax^2 + Bx + C$ ，那么这个二次方程的解的 $x$ 值就是在 $y=0$ 处的“交点”。因为 $y = Ax^2 + Bx + C$ 是一条抛物线，根据抛物线是否偏离、擦过或碰到 x 轴，这个二次方程会有 $0$ 、 $1$ 或 $2$ 个实数解 [图 2-5] 。

图 2-5

为了求二次方程的解析解，我们首先同除 A：

\[x^2 +\frac{B}{A}x+\frac{C}{A} = 0\]

然后我们配成“完全平方”项，来给项分组：

\[\left( x+\frac{B}{2A}\right)^2 - \frac{B^2}{4A^2} +\frac{C}{A} = 0\]

把常数部分移到右边，然后开方。得到：

\[x+\frac{B}{2A} = \pm \sqrt{\frac{B^2}{4A^2} - \frac{C}{A}}\]

两边同时减去 $\frac{B}{2A}$ ，以 $2A$ 为分母，得到熟悉的求根公式：

\[x = \frac{-B\pm \sqrt{B^2-4AC}}{2A} \tag{2.1}\]

这里的“ $\pm$ ”符号表示有两个解，一个带正号，一个带负号。因此， $3±1$ 等于“ $2$ 或 $4$ ”。注意，决定实解个数的项是 $D \equiv B^2-4AC$ 。这也叫做这被称为二次方程的 判别式 。如果 $D > 0$ ，则有两个实数解（也称为根）。如果 $D = 0$ ，则存在一个实解（称作“二重”根）。如果 $D < 0$ ，则不存在实解。

2.3 三角函数学

在图形学中，我们在很多情况下使用基本的三角函数。通常，图形学不会用太花哨的公式，而且图形学的知识有助于记住三角学的基本定义。

2.3.1 角度与弧度

虽然我们认为角度是理所当然的，但我们应该回到它们的定义上来，这样我们就可以把角度的概念扩展到球体上。夹角是在两条 半线 （来自一个原点的无限射线）或方向之间形成的，因此必须使用一些惯例来决定它们之间形成夹角的两种可能性，如 [图 2-6] 所示。一个角是由它在单位圆上切出的弧段的长度来定义的。我们使用两条射线之间较小的弧长来定义角度，角度的符号由指定两条半线的顺序决定。根据这个惯例，所有的角都在 $[−π， π]$ 的范围内。

图 2-6 图 2-7

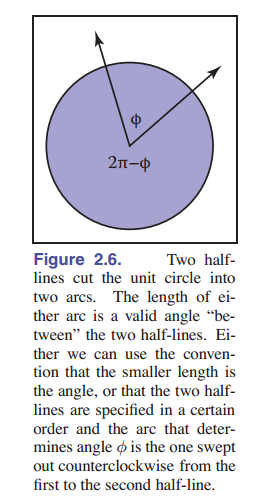
每一个角都是 被两个方向“切割”的单位圆的弧的长度 。因为单位圆的周长是 $2π$ ，这两个可能的角和等于 $2π$ 。弧长的单位是弧度。另一个常用的单位是度，圆的周长是 $360$ 度。因此，一个 $π$ 弧度的角是 $180$ 度，通常表示为 $180°$。度和弧度之间的转换是：

\[{\rm degrees} \ = \frac{180}{\pi} {\rm radians}\] \[{\rm radians} \ = \frac{\pi}{180} {\rm degrees}\]

2.3.2 基础三角函数

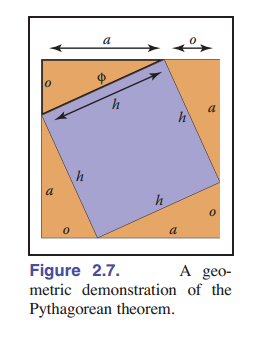
给定一个边长为 $a$ 、$o$ 和 $h$ 的直角三角形，其中 $h$ 是最长的边（是直角的对边）或斜边的长度，勾股定理描述了一个重要的关系：

\[a^2+o^2 = h^2\]

你可以从 [图 2-7] 中看到这是正确的，其中大正方形的面积为 $(a+o)^2$ ，四个三角形的总面积为 $2ao$ ，中心正方形的面积为 $h^2$ 。

针对一个角度 $\phi$ ，我们定义它的 正弦 和 余弦 ，以及其他基于比例的三角函数表达式：

\(\sin \phi ≡ o/h;\) \(\csc \phi ≡ h/o;\) \(\cos \phi ≡ a/h;\) \(\sec \phi ≡ h/a;\) \(\tan \phi ≡ o/a;\) \(\cot \phi ≡ a/o;\)

基于这些定义，我们可以引出另外一种坐标表达形式：极坐标，其中一个点的位置由两个参数决定：离原点的距离 和 相对于正 $x$ 轴的带符号角度（[图 2-8]）。请注意，角的范围是 $\phi \in (−\pi， \pi)$ ，角度为正的意思是 与正 $x$ 轴方向成逆时针。我们在图形学中的许多定义中都会用到逆时针为正的定义，值得记一记。

图 2-8 图 2-9

三角函数是周期性的，因此可以取任意角度作为参数。例如， $\sin(A) = \sin(A + 2\pi)$ 。这意味着当考虑定义域 $\mathbb{R}$ 时，三角函数不可逆。不过这个问题可以通过限制标准反函数的范围来避免，这在几乎所有现代数学库中都成为了一个标准，并有实现。如(Plauger, 1991)）。下面列出了一些反三角函数的定义域和值域：

\({\rm asin} : [-1,1] \mapsto [-\pi /2, \pi/2];\) \({\rm acos} : [-1,1] \mapsto [0, \pi];\) \({\rm atan} : \mathbb{R} \mapsto [-\pi /2, \pi/2];\) \({\rm atan2} : \mathbb{R} \mapsto [-\pi /2, \pi/2];\)

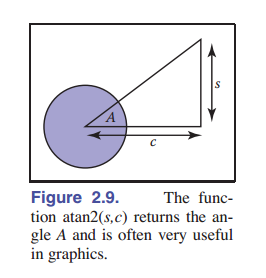
最后一个函数 ${\rm atan2}(s, c)$ 通常非常有用。针对一个直角三角形，它取一个角的对边 $s$ ，以及一个邻边 $c$ 作为输入。函数 ${\rm atan2}(s,c)$ 计算出角度 A 并返回。这在图形学中非常有用。假设因子是正的。我们可以这样看这个运算：它在极坐标中返回二维笛卡尔坐标中 $(s, c)$ 对应的角度 $A$ ，如 [图 2-9] 。

2.3.3 有用的三角函数转换公式

三角函数的互转公式：

\[\begin{align*} \sin(−A) &= − \sin A \\ \cos(−A) &= \cos A \\ \tan(−A) &= − \tan A \\ \sin(\pi/2−A) &= \cos A \\ \cos(\pi/2−A) &= − \sin A \\ \tan(\pi/2−A) &= \cot A \\ \end{align*}\]

倍角公式、和差角公式：

$\tan:$

\[\tan(\alpha\pm\beta)=\cfrac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\] \[\tan2\alpha=\cfrac{2\tan\alpha}{1-\tan^2\alpha}\]

$\sin:$

\[\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\] \[\sin2\alpha=2\sin\alpha\cos\alpha\] \[\sin2\alpha=\cfrac{2\tan\alpha}{1+\tan^2\alpha}\]

$\cos:$

\[\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\] \[\cos2\alpha=\cos^2\alpha-\sin^2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha\]

正弦公式：

\[\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}\]

余弦公式：

\[c^2 = a^2+b^2-2ab\cos C\]

正切公式：

\[\frac{a+b}{a-b} = \frac{\tan(\frac{A+B}{2})}{\tan(\frac{A-B}{2})}\]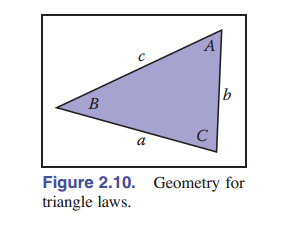

图 2-10

三角形面积公式：

\[S=\frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}\]

2.4 向量

什么，你是九漏鱼？那请坐等作者翻译完之后的更新。 —— 译者

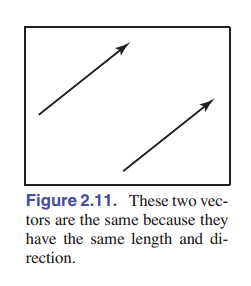
向量 是一个描述了长度和方向的量。向量的图形一般通过箭头表示。如果有两个向量，他们长度相同，指向的方向相同，但是位置不同，我们也认为这是相同的向量。如 [图 2.11] 。尽管我们在程序中表示向量用的是数字，但向量更像是一个箭头，而不是坐标或数字。我们操作向量的时候也应该将它视为一个对象，而非一个数。向量的表示使用粗体正体字母，如 $\mathbf{a}$ ，向量的长度表示为 $\parallel\mathbf{a}\parallel$ 。 单位向量 是长度为 1 的向量。 零向量 是长度为 $0$ 的向量，零向量没有方向。

向量可以表示很多东西。如，通过向量可以表示 偏移量 （也称 位移 ）。如果我们知道“宝藏埋在一个地方向东两步，向北三步的地方”，那么我们就知道了偏移量，但我们不知道从哪里开始。与此同时，向量也可以用来存储位置，也就是 位置坐标 。当一个向量作为位置表示时，我们可以将其定义为 相对于原点的位移 。通常我们会定义一个原点位置，所有其他位置都以偏移量的形式存储。请注意，位置不是向量。正如我们将要讨论的，你可以将两个向量相加，这代表两次位移作用的结果。但是，两次位置的平均是没有意义的，除非你是在计算一个位置的 加权平均 ，作为某个步骤的中间操作(Goldman, 1985)。与此相对，添加两个偏移量是有意义的，这也就是偏移量是向量的原因之一。

图 2-11 图 2-12

2.4.1 向量操作

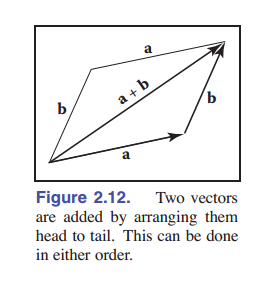
向量支持大多数实数的算术运算。我们定义：当且仅当两个向量有相同的长度和方向，两个向量相等。向量的加法遵循平行四边形法则。也就是说，两个向量的和是通过将任意一个向量的尾部与另一个向量的头部相接得到的（ [图 2-12] ）。它们的和向量是由这两个向量构成的“三角形斜边”的这一向量。加法可以用任意的顺序，也就是说向量加法是可交换的：

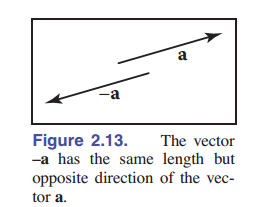
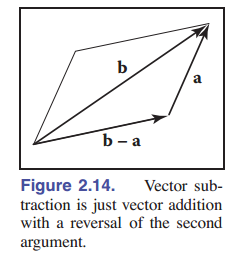
\[\mathbf{a}+\mathbf{b} = \mathbf{b}+\mathbf{a}\]

除此之外，我们还可以定义一个 一元减号 ： $-\mathbf{a}$ 向量与 $\mathbf{a}$ 向量等长、但反向。由此减法就定义出来了：

\[\mathbf{b}-\mathbf{a} \equiv -\mathbf{a}+\mathbf{b}\]

向量也可以相乘。实际上，有多种与向量相关的乘积。首先我们说 数乘 ，我们可以将向量乘以一个实数 $k$ 。它的效果是将 $k$ 乘以向量的长度，但不改变它的方向。例如， $3.5\mathbf{a}$ 是与 $\mathbf{a}$ 方向相同的向量，但它是 $\mathbf{a}$ 的 $3.5$ 倍长。我们将在本节后面讨论涉及两个向量的两个乘积，即点积和叉积，并在第五章讨论涉及三个向量的乘积，即 行列式 。

图 2-13 图 2-14

2.4.2 向量的笛卡尔坐标

二维向量可以写成任意两个不平行的非零向量的组合。这两个向量的性质叫做 线性无关 。两个线性无关的向量构成一个二维 基 ，这两个向量构成一个平面，然后这个平面内的所有向量都可以用这两个向量组合得到。因此这两个向量被称为 基向量 。例如，向量 $\mathbf{c}$ 可以表示为两个基向量 $\mathbf{a}$ 和 $\mathbf{b}$ 的组合 ([图 2-15]):

\[\mathbf{c} = a_c \mathbf{a} + b_c \mathbf{b}. \tag{2.3}\]

注意，权重 $a_c$ 和 $b_c$ 是唯一的。如果两个向量是正交的，即它们彼此成直角，基就更加有用。如果它们也是单位向量的话，那就更方便了。在这种情况下，我们称它们是 标准正交 的。如果我们假设两个这样的“特殊”向量 $\mathbf{x}$ 和 $\mathbf{y}$ 是已知的，那么我们可以用它们来表示 笛卡尔坐标系 中的所有其他向量，其中每个向量都用两个实数表示。例如，向量 $\mathbf{a}$ 可以表示为：

\[\mathbf{a} = x_a \mathbf{x} + y_a \mathbf{y}\]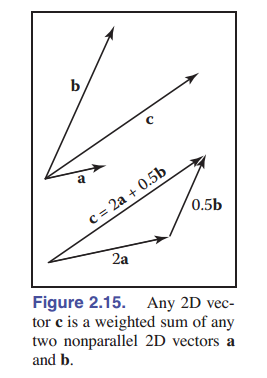

图 2-15 图 2-16

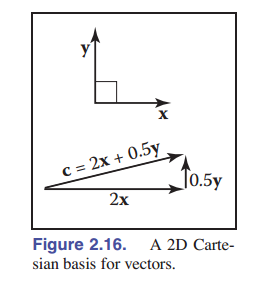
这里的 $x_a$ 和 $y_a$ 就是一个二维笛卡尔坐标（[图 2-16]） 。 请注意，这在概念上与 公式(2.3) 没有任何不同，只不过 公式(2.3) 中的基向量不是标准正交的。但是笛卡尔坐标系有几个优点。例如，根据勾股定理， $\mathbf{a}$ 的长度很容易计算：

\[\parallel\mathbf{a}\parallel = \sqrt{x_a^2+y_a^2}.\]

在笛卡尔坐标系中计算点积、叉积和向量坐标也很简单，我们将在接下来的章节中看到。

按照惯例，我们将 $\mathbf{a}$ 的坐标写成有序对 $(x_a, y_a)$ ，或写成一个列矩阵：

\[\mathbf{a} = \left [ \begin{matrix} x_a \\ y_a \\ \end{matrix} \right]\]

我们使用的形式将取决于排版的便利性。我们偶尔也会把这个向量写成行矩阵，然后加一个转置符号，我们用 $\mathbf{a}^T$ 表示：

\[\mathbf{a}^{\rm T} = \left [ \begin{matrix} x_a & y_a \\ \end{matrix} \right]\]

我们也可以用笛卡尔坐标表示三维、四维等向量。对于三维情况，我们多使用一个基向量 $\mathbf{z}$ ，它与 $\mathbf{x}$ 和 $\mathbf{y}$ 都正交。

2.4.3 向量点积

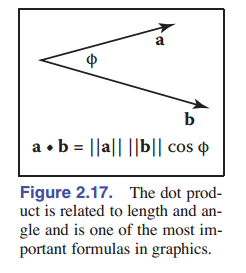
两个向量相乘最简单的方法是 点积 。 $\mathbf{a}$ 和 $\mathbf{b}$ 的点积表示为 $\mathbf{a} \cdot \mathbf{a}$ ，通常称为 标量积 ，因为它返回一个标量。点积返回的值与这两个参与运算的向量的长度、以及它们之间的夹角 $\phi$ 有关。（ [图 2.17] ）

\[\mathbf{a} \cdot \mathbf{b} = \parallel \mathbf{a}\parallel \parallel \mathbf{b}\parallel \cos \phi , \tag{2.4}\]

点积在图形程序中最常用的用法是计算两个向量夹角的余弦值。

点积也可以用来求一个向量在另一个向量上的投影。$\mathbf{a} \to \mathbf{b}$ 是向量 $\mathbf{a}$ 作垂线，投影到向量 $\mathbf{b}$ 上的长度。( [图 2.18] )：

图 2-17 图 2-18

\[\mathbf{a} \to \mathbf{b} = \parallel\mathbf{a}\parallel \cos \phi = \frac{\mathbf{a}\cdot\mathbf{b}}{\parallel\mathbf{b}\parallel} \tag{2.5}\]

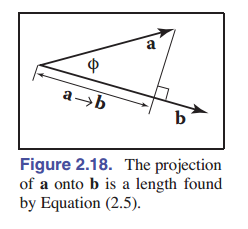
点积也遵循我们在实数算术中的结合律和分配律：

\(\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}\) \(\mathbf{a} \cdot (\mathbf{b}+\mathbf{c}) = \mathbf{a} \cdot \mathbf{b}+ \mathbf{a}\cdot \mathbf{c} \tag{2.6}\) \((k\mathbf{a}) \cdot \mathbf{b} = \mathbf{a} \cdot (k\mathbf{b}) = k\mathbf{a}\cdot\mathbf{b}\)

如果二维向量 $\mathbf{a}$ 和 $\mathbf{b}$ 用笛卡尔坐标表示，我们可以利用 $\mathbf{x}·\mathbf{x} = \mathbf{y}·\mathbf{y} = 1$ 和 $\mathbf{x}·\mathbf{y} = 0$ 来推导出它们的点积计算公式：

\[\begin{align*} \mathbf{a} \cdot \mathbf{b} &= (x_a\mathbf{x}+y_a\mathbf{y}) \cdot (x_b\mathbf{x}+y_b\mathbf{y}) \\ &= x_ax_b(\mathbf{x}\cdot\mathbf{x})+x_ay_b(\mathbf{x}\cdot\mathbf{y})+x_by_a(\mathbf{y}\cdot\mathbf{x})+t_ay_b(\mathbf{y}\cdot\mathbf{y}) \\ &= x_ax_b+y_ay_b \\ \end{align*}\]

三维也一样，有：

\[\mathbf{a} \cdot \mathbf{b} = x_ax_b+y_ay_b+z_az_b\]

2.4.4 向量叉积

向量叉积一般只用于三维向量。我们使用右手定则确定方向，向量的长度和夹角有关：

\[\parallel\textbf{a}\times\textbf{b}\parallel=\parallel\textbf{a}\parallel\parallel\textbf{b}\parallel\sin\phi.\]

$\mathbf{a}\times\mathbf{b}$ 的大小等于向量 $\mathbf{a}$ 和 $\mathbf{b}$ 构成的平行四边形的面积。另外， $\mathbf{a} \times \mathbf{b}$ 垂直于 $a$ 和 $b$ ( [图 2-19] ) 。注意，对于叉积的结果向量的方向，只有两个可能。我们通过右手法则来判断方向。除大拇指外的手指从 $\mathbf{a}$ 弯向 $\mathbf{b}$ ，大拇指所指的位置就是 $\mathbf{a} \times \mathbf{b}$ 的方向 （[图 2-20]）。三维笛卡尔坐标轴也由此定义：

图 2-19 图 2-20

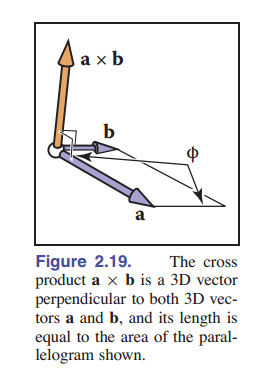
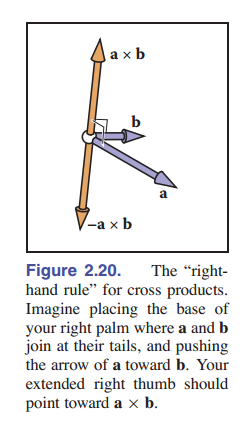
\(\mathbf{x} \times \mathbf{y} = +\mathbf{z},\) \(\mathbf{y} \times \mathbf{x} = -\mathbf{z},\) \(\mathbf{y} \times \mathbf{z} = +\mathbf{x},\) \(\mathbf{z} \times \mathbf{y} = -\mathbf{x},\) \(\mathbf{z} \times \mathbf{x} = +\mathbf{y},\) \(\mathbf{x} \times \mathbf{z} = -\mathbf{y}.\)

向量的叉积有如下性质（结合律、数乘）：

\(\mathbf{a} \times (\mathbf{b}+\mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c}\) \(\mathbf{a} \times (k\mathbf{b}) = k(\mathbf{a} \times \mathbf{b})\)

但是，由于使用了右手定则，叉积没有交换律：

\[\mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a})\]

在笛卡尔坐标系中，我们可以使用显式展开来推导出叉乘的公式：

\[\begin{align*} \mathbf{a} \times \mathbf{b} &= (x_a\mathbf{x}+y_a\mathbf{y}+z_a\mathbf{z}) \times (x_b\mathbf{x}+y_b\mathbf{y}+z_b\mathbf{z}) \\ &= x_ax_b\mathbf{x}\times \mathbf{x} + x_ay_b\mathbf{x}\times \mathbf{y}+ x_az_b\mathbf{x}\times \mathbf{z} \\ &+y_ax_b\mathbf{y}\times \mathbf{x}+y_ay_b\mathbf{y}\times \mathbf{y}+y_az_b\mathbf{y}\times \mathbf{z} \\ &+z_ax_b\mathbf{z}\times \mathbf{x}+z_ay_b\mathbf{z}\times \mathbf{y}+z_az_b\mathbf{z}\times \mathbf{z} \\ & = (y_az_b-z_ay_b)\mathbf{x} +(z_ax_b-x_az_b)\mathbf{y}+(x_ay_b-y_ax_b)\mathbf{z} \tag{2.7} \end{align*}\]

因此，写成坐标形式，向量叉积的公式是

\[\mathbf{a} \times \mathbf{b} = (y_az_b-z_ay_b,z_ax_b-x_az_b,x_ay_b-y_ax_b) \tag{2.8}\]

2.4.5 规范正交基和坐标系

所有图形程序中，坐标系统都是其核心。坐标系统的核心则是正交基。要想作为正交基，两个二维向量必须垂直且都是单位长度。即：

\[\parallel u\parallel=\parallel v \parallel =1,\] \[u\cdot v=0.\]

在三维空间，需要满足

\[\parallel u\parallel=\parallel v \parallel =\parallel w \parallel =1,\] \[u\cdot v=v\cdot w=w\cdot u=0.\]

同时，这个坐标系采用右手系：

\[\mathbf{w}=\textbf{u} \times \textbf{v},\]

请注意，笛卡尔直角坐标系只是很多很多坐标系中的一种。它的特殊之处在于图形程序中的低级（默认）表示都是用该坐标系表示的。因此，基向量 $\mathbf{x},\mathbf{y},\mathbf{z}$ 和原点 $\mathbf{o}$ 都不是显式存储的，是默认就规定好的。全局模型通常存储在规范坐标系中，所以我们又将这个坐标系称为 全局坐标系统 。然而，如果我们想要将原点换成 $\mathbf{p}$ 点，正交基换成 $\mathbf{u},\mathbf{v},\mathbf{w}$ ，那么我们就需要显式地存储这些向量和点。这样的坐标系统叫 参考系 。举个例子：在飞行模拟器中，我们可能就会需要既有一个在原点在机头、顺着飞机方向建立基向量的坐标系，同时又需要一个主要坐标系，主要坐标系一般围绕一个不是飞机的特定物体建立，一般称作 局部坐标系 。

图 2-21

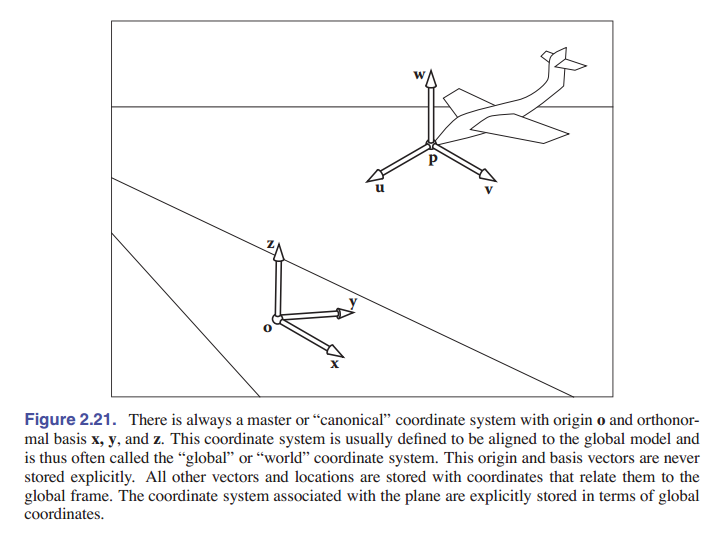
在底层，本地坐标系一般依据规范坐标建立，比如，假设 $a$ 有在 u-v-w 坐标系下有坐标 $(x_a,y_a,z_a)$ ，那么它在规范坐标系下的表示就是：

\[\rm{\textbf{u}}=x_a\rm{\textbf{u}}+y_a\rm{\textbf{v}}+z_a\rm{\textbf{w}}\]

2.4.6 通过单个向量来生成基坐标

我们建立坐标系的限制条件有时只有一个。比如，限定 z 轴正方向是飞机的飞行方向。所以通过单个向量生成基坐标的步骤如下：

首先取限定向量 $\mathbf{w}$ 的单位向量做方向： \(\rm\textbf{w} = \frac{\textbf{a}}{\parallel\textbf{a}\parallel}.\)

然后找一个任意不共线的向量 $\rm\textbf{w}$，将他们叉乘取出另外一个轴方向。

\[\mathbf{u} = \frac{\textbf{t}\times \textbf{w}}{\parallel\textbf{t}\times \textbf{w}\parallel}.\]

如果 $\mathbf{t}$ 和 $\mathbf{w}$ 共线，那么叉乘向量就是零向量，如果近乎共线，那么坐标轴就会缺少精度。解决这个问题的一种好办法就是，先构造两个相同向量，如 $w=(1/\sqrt{2},-1/\sqrt{2},0)$ ，然后将 $0$ 改成 $1$ ，即 $t=(1/\sqrt{2},-1/\sqrt{2},1)$ 。

在表面阴影的生成时，这样的办法比较好用，因为此时需要一个带有表面法向量方向的坐标系，但其他条件并不重要。

2.4.7 通过两个向量构造基向量

有一种情况很重要：基绕着给定向量旋转。一个常见的例子是相机创建的基坐标：让一个矢量与相机所看的方向对齐，但除此之外，我们还需要以某种方式指定其他向量。只有确定了相机的方向，才能完全确定一个基。

一个常用的方法来完全指定一个坐标系是通过提供两个向量 $\mathbf{a}$ （这能确定相机坐标中的 $\mathbf{w}$ ）；以及 $\mathbf{b}$ （这能指定相机坐标中的 $\mathbf{v}$ ）。如果已知这两个向量是垂直的，那么我们可以直接用 $\mathbf{u}=\mathbf{b} \times \mathbf{a}$ 来构造第三个向量。

为了确保结果基确实是标准正交的，即使输入向量不是完全正交的，也建议使用类似于单向量生成坐标系的过程：

\(\mathbf{w} = \frac{\mathbf{a}}{\parallel\mathbf{a}\parallel}\) \(\mathbf{u} = \frac{\mathbf{b} \times \mathbf{w}} {\parallel\mathbf{b} \times \mathbf{w}\parallel}\) \(\mathbf{v} = \mathbf{w} \times \mathbf{u}\)

实际上，当 $\mathbf{a}$ 和 $\mathbf{b}$ 不垂直时，这个方法也能成功。在这种情况下， $\mathbf{w}$ 也会在 $\mathbf{a}$ 的方向上构造出来，并且在所有垂直于 $\mathbf{w}$ 的向量中离 $\mathbf{b}$ 最近的向量就是 $\mathbf{v}$。

当心！如果 $\mathbf{a}$ 和 $\mathbf{b}$ 共线了，这个方法就不能用了。因为这样第二步的叉乘会无法运行，得到零向量。

在指定摄像机位置的例子中 ([4.3 节]) ，我们想要构建一个 $\mathbf{w}$ ，描述摄像机所看方向，并且 $\mathbf{v}$ 应该指向摄像机的顶部。为了使摄像机垂直定向，我们围绕视角方向建立基，以 $z$ 轴作为参考向量，围绕视角方向建立摄像机的方向。将 $\mathbf{v}$ 设置得尽可能接近垂直，正好符合“保持相机垂直”的直觉概念。

2.4.8 重新生成基向量

有些时候你会发现你算出来的规范正交基是有问题的：由于计算机会进行舍入操作或者存储时精度过低，这造成了所谓的规范正交基既不规范（可能和 $1$ 相差一点距离），也不正交（可能和 $90°$ 相差一点角度）。

所以前一节的知识可以派上用场了：我们只需要将已存在的 $\mathbf{w}$ 和 $\mathbf{v}$ 这两个向量重新叉乘生成新的规范正交基即可。

这种方法非常实用，但是它的效果并不是最好的，尽管它能提供准确的正交向量，但它对三个基向量的侧重程度不同。它在 $\mathbf{uvw}$ 中对 $\mathbf{w}$ 的优先级最高，其次是 $\mathbf{v}$ ，然后是 $\mathbf{u}$ 。它在创建基向量是有明显的倾向性，同时也不能保证计算出来的正交基就是最标准的规范正交基。当然这有解决办法。在 5.4.1 节中，我们会讲到 SVD 方法（奇异值分解），它能找到和原来的基向量最接近的规范正交基。

2.5 曲线和曲面

曲线和曲面，尤其是对表面的几何分析，是计算机图形学的中心问题。现在我们来康康 2D 和 3D 中的曲线和曲面。 讲前提醒：隐式和显式的表示方式大不相同，如：隐式表示方式适合判断一个点是否在曲面内。

2.5.1 二维隐式曲线

显而易见的，曲线 是一系列能够一笔画成的点。通常我们用 隐函数 来表示曲线。二维的隐函数是这样的：

\[f(x,y) = 0.\]

函数 $f(x,y)=0$ 返回一个实数。使得该函数值为 0 的所有点 $(x,y)$ 组成一条曲线。由于 $f$ 对所有 $(x,y)$ 都有值，所以可以通过曲线形成一一块区域。下面的式子：

\[f(x,y) = (x-x_c)^2+(y-y_c)^2-r^2=0\]

写成向量的形式则是：

\[(\rm\textbf{p}-\textbf{c})\cdot(\textbf{p}-\textbf{c}-r^2=0)\]

其中 $\mathbf{p}=(x,y)$ , $\mathbf{c}$ 是某点 $(x_c,y_c)$ 。

图 2-22 图 2-23

更直观的，那俩平方其实就是距离：

\[\parallel {\rm\textbf{p}-\textbf{c}}\parallel^2-r^2 = 0\]

我们更建议你使用向量等式，因为它更符合几何定义，也更直观；另外你还可以在代码中引入向量，让代码更易读，同时产生更少的错误。学会使用向量，刚开始可能有点难，但之后会让你事半功倍。

2.5.2 二维梯度

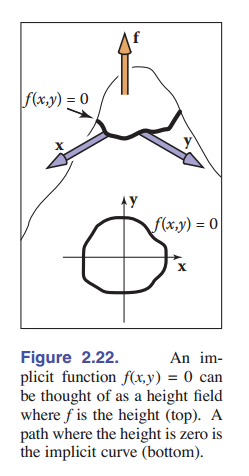
如果我们将函数 $f(x,y)$ 视作高度函数，即 ${\rm height} = f(x,y)$ , 那么它的 梯度 就是只想最大向上斜率的一个向量（换句话说，就是朝着上坡方向）。梯度向量由以下公式给出：

\[\nabla f(x,y) = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}).\]

我们使用 $\nabla$ 表示梯度。

在隐式曲面 $f(x,y)$ 的某一点上的梯度向量是垂直于曲线在该点处的 切向量。这个垂直的向量我们一般叫做曲面的 法向量 。而且，因为梯度指向更高的地方，说明沿着梯度方向更上面的那块地方的函数值 $f(x,y)>0$ 。

图 2-24

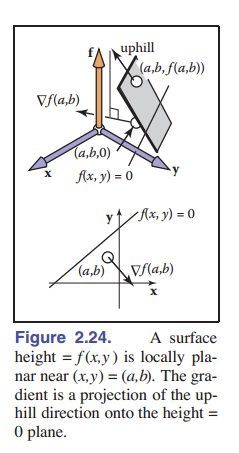
在 $f$ 作为高度函数的内容中，偏导和梯度的几何意义更直观的可以看出。假设在 $(a,b)$ 点附近有一个平面 $f(x,y)$ ，（见 [图 2-24] ），这个平面有很特定的上坡下坡的方向。而从与该方向垂直的方向上看这个平面，平面是一条直线。平面 $f(x,y)$ 和线 $f(x,y)=0$ 之间的交点都将位于水平方向。那么为啥偏导数与此有关呢？让我们看看几何图像。我们学过，一维函数 $y=g(x)$ 的导数是：

\[\frac{dy}{dx} = \lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0}\frac{g(x+\Delta x)-g(x)}{\Delta x}\]

这同时也是该曲线在 $x$ 处的斜率。

图 2-25 图 2-26

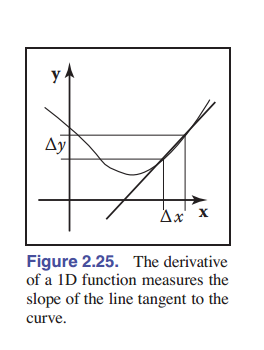
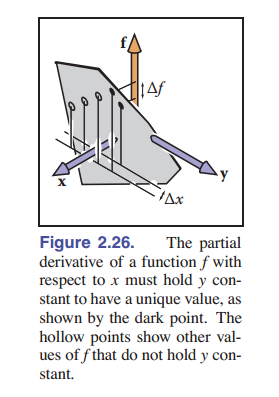
偏导数是一维导数的推广。对于一个二维函数 $f(x,y)$ ，我们不能单纯的用上面的极限来定义二元导数，因为当 $x$ 不变时，函数值也会发生变化。但是，我们可以引申出 偏导 这一概念，让 $y$ 视为常数，就有下面的式子：

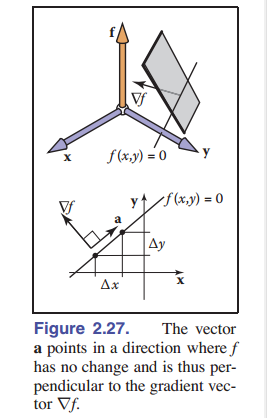
\[\frac{\partial f}{\partial x} = \lim_{\Delta x \to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}\]

为什么梯度向量的两个成员分别是 x 和 y 的偏导呢？同样，让我们看更直观的图像：在 [图 2-27] 中，我们看到向量 $\rm a$ 的路径上 f 的值一直不变。由于 $\Delta x$ 意味着是在一个足够小的范围，所以该区域可以视为平面。在图上能看到，向量 ${\rm a}=(\Delta x,\Delta y).$ 同时由于上坡方向和向量 $\rm a$ 垂直，所以点积为 0：

\[(\nabla f)\cdot a \equiv (x_\nabla,y_\nabla)\cdot(x_a,y_a) = x_\nabla\Delta x+y_\nabla\Delta y = 0.\]

同时，上一段话提到沿着 $\rm a$ 方向上的变化率是 $0$ ，有：

\[\Delta f = \frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y\equiv \frac{\partial f}{\partial x}x_a+\frac{\partial f}{\partial y} y_a = 0.\]

通过垂直向量点积为 $0$ 的结论，结合上面的两个等式，我们有：

\[(x_a,y_a) = k(\frac{\partial f}{\partial y},-\frac{\partial f}{\partial x})\]

同时有：

\[(x_\nabla,y_\nabla) = k'(\frac{\partial f}{\partial y},-\frac{\partial f}{\partial x})\]

其中 $k$ 和 $k’$ 是非零常数。由于“上坡”意味着 $f$ 增大，所以我们可以让 $k’=1$ .

举个梯度的例子，比如圆的方程 $x^2+y^2-1=0$ ,容易算出梯度向量是 $(2x,2y)$ . 这说明了对于函数 $f(x,y) =x^2+y^2-1$ ,在该圆外面的区域是正区域。需要注意的是，带乘二系数的圆方程： $2x^2+2y^2-2=0$ 和先前的圆是同一个，但是梯度为 $(4x,4y)$ 。不同的方程样式可能会导致梯度向量的长度发生变化。而对于系数是负数的圆，在三维空间看 $f(x,y)$ ，圆内的形状是凸起的，所以可以统一地讲， 梯度的长度反应了坡度变化的快慢，梯度的方向指向上坡方向 。

图 2-27 图 2-28

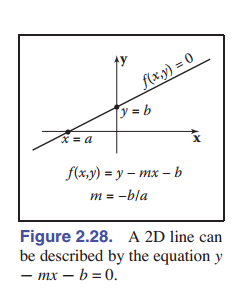
二维空间直线的隐式表示

直线的表示方式是： \(y = mx + b,\) 即 \(y − mx − b = 0.\)

其中 $m$ 是斜率，$b$ 是直线穿过 $y$ 轴的 $y$ 轴处坐标，称为 y 轴截距 。我们可以将他把平面分成的两个部分称为上部和下部。

我们引入了 一般式 ，为了防止像 $x=0$ 这样的方程用截距式无法表示：

\[Ax+By+C=0\]

其中 A、B、C 均为实数。

如果说，我们知道直线的两个点 $(x_0,.y_0)$ , $(x_1,y_1)$ ,我们可以列出式子：

\(Ax_0+By_0+C=0\) \(Ax_1+By_1+C=0\)

但这样会产生三个未知数和两个方程。我们可以将方程同除 $C$ ，得到：

\[Ax+By+1=0\]

同样这也有问题，而且是和截距式类似的问题，那就是没法表示 $x=y$ 这样的直线。

当我们遇到麻烦的代数问题时，我们可以尝试通过数形结合来直观的解决问题。我们在 [2.5.2 节] 讲过，对于直线 $Ax+By+C=0$ ，它的梯度向量是 $(A,B)$ . 同时这个向量和直线垂直，指向直线上侧，也就是 $Ax+By+C>0$ 一侧。在直线上取两个点构成一个向量，显然这个向量的方向就是直线的方向，同时垂直与梯度向量。

图 2-29

我们将这两点设为 $(x_0,y_0)$， $(x_1,y_1)$ ，那么这条直线方程又可以写成： \((y_0-y_1)x+(x_1-x_0)y+C=0\)

那么我们只要把 $C$ 解出来就好了。其实，只需要代入这条直线上的一个点即可，代入 $(x_0,y_0)$ ，可以得到：

\[(y_0-y_1)x+(x_1-x_0)y+x_0y_1-x_1y_0=0\]

这个方程就不会有之前那样的局限性了，而且可以很容易的转化成截距式：

\[y-\frac{y_1-y_0}{x_1-=x_0}x+\frac{x_1y_0-x_0y_1}{x_1-x_0}\]

图 2-30 图 2-31

使用一般式，我们也可以求点到直线的距离。若有一个点 $(a,b)$，直线 $Ax+By+C=0$ ,

\[{\rm distance} =\frac{f(a,b)}{\sqrt{A^2+B^2}}\]

距离恒正。但计算结果可能为负，此时需要额外进行绝对值处理，或采用以下推导出来的公式：

\[f(x,y)=\frac{y_0-y_1}{\sqrt{(x_1-x_0)^2+(y_0-y_1)^2}}x+\frac{x_1-x_0}{\sqrt{(x_1-x_0)^2+(y_0-y_1)^2}}y+\frac{x_0y_1+x_1y_0}{\sqrt{(x_1-x_0)^2+(y_0-y_1)^2}}\]

该公式通过确保 $(A,B)$ 是单位向量来简化计算。

直接计算 $f(x,y)$ 的值就是点和线的恒正距离。

隐式直线对三角形光栅化会很有帮助( [8.1.2 节] )。在 [第 14 章] ，我们会讨论二维直线的其他表示形式。

隐式二次曲线

上面介绍了线性函数 $f(x,y)$ 可以构造一个隐式直线 $f(x,y)=0$ 。但如果 $f$ 是一个二次函数，标准型如下：

\[Ax^2+Bxy+Cy^2+Dx+Ey+F=0\]

那么它生成的曲线叫二次曲线。二维的二次曲线包括椭圆和双曲线，在特殊情况下，会变成抛物线、圆、直线。二次曲线的例子有：圆心为 $(x_c,y_c)$ 的圆： \((x − x_c)^2 + (y − y_c)^2 − r^2 = 0,\)

图 2-32

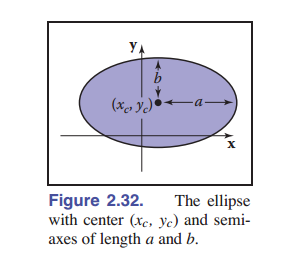
轴对齐的椭圆： \(\frac{(x-x_c)^2}{a^2}+\frac{(y-y_c)^2}{b^2}\)

轴对齐指椭圆的长轴短轴分别和坐标轴 $x$ 、 $y$ 对齐。

椭圆圆心为 $(x_c,y_c)$ ，长轴短轴分别是 $a$ 和 $b$。

2.5.3 三维隐式曲面

正如隐式方程在二维空间中可以定义一条曲线，三维空间中它能定义一个曲面。就像在二维空间那样，隐式方程描述了在这个表面上的所有点的集合。我们也可以将该函数写成向量表示法： $\rm\textbf{p}=(x,y,z)$, $f(\rm\textbf{p})=0$ .

2.5.4 隐式曲面的表面法线

表面法线（用于光线计算和其他）是一个垂直于表面的向量。由于曲面是弯曲的，每个点都有可能会有不同的法向量。和二维一样，某点$P$的表面法线 $\mathbf{n}$ 通过梯度来表示：

\[{\mathbf{n}} = \nabla f({\mathbf{p}}) = (\frac{\partial f({\mathbf{p}})}{\partial x},\frac{\partial f({\mathbf{p}})}{\partial y},\frac{\partial f({\mathbf{p}})}{\partial z})\]

这样表示的依据和二维例子一样。梯度指明了 $f$ 增长最快的方向，所以是垂直于平面上所有切线的，其中 f 保持不变。梯度向量始终指向 $f(p)>0$ 的方向。在几何上则是朝着曲面内/外的描述方法。如果 $f$ 算出来的梯度向内，而我们需要向外的梯度，那么曲面 $f(\mathbf{p})$ 和 $-f(\mathbf{p})$ 会有方向相反、大小相同的梯度。

2.5.5 隐式平面

举个例子，假设有一个无限大的平面，点 $\mathbf{a}$ 是平面上的一点，平面的法向量是 $\mathbf{n}$ ,那么这个平面就可以通过下式表示：

\[(\mathbf{p}- \mathbf{a})\ \cdot \mathbf{n}= 0\]

其中 $\mathbf{a}$ 和 $\mathbf{n}$ 已知，点 $\mathbf{p}$ 是平面上的任意点。在几何上，该式子的意思是：平面内任取两个点，该向量都和法向量垂直。推理可得，如果点 $\mathbf{p}$ 不在平面里，组成的向量也就不会和法向量垂直。

图 2-33

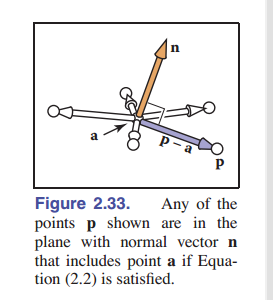
有时候我们会需要通过三个点 $\mathbf{a}$ 、 $\mathbf{b}$ 、 $\mathbf{c}$ 确定一个平面，然后寻找它的法向量。这很简单，只需要利用向量的叉乘即可： \(\mathbf{n}=(\mathbf{b}- \mathbf{a})\times (\mathbf{c}- \mathbf{a})\)

所以隐式平面的方程也可以得出来： \((\mathbf{p}-\mathbf{a})\cdot((\mathbf{b}- \mathbf{a})\times (\mathbf{c}- \mathbf{a})) = 0\)

同样我们来解释一下上面式子的意思。根据 向量混合积 的定义，这个式子的意思是：由 $\mathbf{p}-\mathbf{a}$, $\mathbf{b}-\mathbf{a}$, $\mathbf{c}-\mathbf{a}$ 这三个向量定义的平行六面体的体积为 $0$ 。也就是说，他们共面。

可以使用行列式来表示上面的等式。行列式给出了完整的笛卡尔表示， [5.3 节] 将对此进行详细讨论。

上面的两种表示方法（向量和行列式等式）都可以实现高效的代码。而如果你将 $x$ 、 $y$ 、 $z$ 三个分量拆开，可能就会产生打字错误，导致臃肿的代码。

三维二次曲面

就像二维里面定义的含有两个变量的二次多项式是表示一条曲线一样，在三维空间中，含有三个变量的多项式定义了空间内的曲面。比如，一个球体可以写成：

\[f(\mathbf{p})=(\mathbf{p}-\mathbf{c})^2-r^2= 0\]

同时，轴对齐的椭球可以写成： \(f(\mathbf{p}) = \frac{(x-x_c)^2}{a^2}+\frac{(y-y_c)^2}{b^2}+\frac{(z-z_c)^2}{c^2}-1=0.\)

从隐式曲面相交而成的三维曲线

我们可能会希望三维曲线是 $f(\mathbf{p}) =0$ 的形式。但是，在三维空间中，这些三维曲线实际上是三维曲面的退化，是在实际当中很少出现的。我们可以通过两个隐式方程的交点来给构造三维曲线：

\[f(\mathbf{p}) = 0\] \[g(\mathbf{p}) = 0\]

比如，可以从两个隐式平面的交点形成三维曲线。一般来说，使用参数化的曲线更方便，后面章节会着重讨论这个问题。

2.5.6 二维参数化曲线

译者注：如果你上过高数/考研数学，就可以快速理解此章。

参数化曲线 指的是由单个参数 $t$ 控制的，由 $t$ 表示 $x$ 和 $y$ 使之平滑移动形成曲线的一种表示方式。如下：

\[\left[\begin{matrix} x \\ y \end{matrix} \right] = \left[\begin{matrix} g(t) \\ h(t) \end{matrix} \right]\]

这里 $(x,y)$ 是曲线上的一个点， $t$ 是影响曲线的参数。对于 $t$ ，函数 $g$ 和 $h$ 会生成一些点，使 $t$ 的变化对 $x$ 和 $y$ 产生连续变化，所以 t 不断变化时，将会绘制出一条曲线。我们通常可以将这样的参数曲线写成向量形式：

$\mathbf{p} = f(t)$, 其中 $f$ 时向量作为变量的函数，映射范围是 $f:\mathbb{R}\to\mathbb{R}$ 。这样的向量函数可以生成非常简洁清爽的代码，所以我们得尽可能用它。

我们可以将曲线的位置看作是一个时间的函数，这条曲线可以任意移动，可以循环、交叉，也可以吧这条曲线看成是在每一个点都有一个自己的速度，如函数 ${\mathbf{p}}(t)$ ，在 $t=-2$ 的时候速度较慢，在 $t=2$ 和 $t=3$ 之间时速度快。我们研究这类参数曲线问题时，为了方便，即使描述的不是动点，我们也可以用动点来描述它。

图 2-34

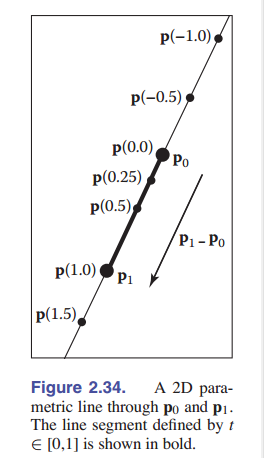
二维参数直线

通过点 $p_0=(x_0,y_0)$ 和 $p_1=(x_1,y_1)$ 的点可以写成：

\[\left[\begin{matrix} x \\ y \end{matrix} \right] = \left[\begin{matrix} x_0+t(x_1-x_0)\\ y_0+t(y_1-y_0) \end{matrix} \right]\]

由于上式的 x 和 y 有相同的结构，我们可以简化为向量形式：

\[{\mathbf{p}}(t) = {\mathbf{p}}_0+t({\mathbf{p}_1-{\mathbf{p}}_0}).\]

你可以将其几何形式理解为：从点 ${\mathbf{p}}_0$ 到 ${\mathbf{p}}_1$ 走了一段距离，距离由参数 $t$ 决定。写成这种形式的一个好处就是 ${\mathbf{p}}(0)={\mathbf{p}}_0$ ， ${\mathbf{p}}(1) = {\mathbf{p}}_1$ ，当这个点随着 $t$ 的变化而变化的时候， $t$ 的值就是两点之间距离的比值。 $t<0$ 说明了点在 ${\mathbf{p}}_0$ 的远侧，而 $t>0$ 说明点在 ${\mathbf{p}}_1$ 的远侧。

参数化的直线也可以写成如下的向量形式：

\[{\mathbf{p}}(t) = {\mathbf{o}}+t({\mathbf{d}}).\]

当向量 ${\mathbf{d}}$ 是单位向量时，直线就是 弧长参数化 的，这表明 $t$就可以用来描述长度。任何参数曲线都可以被弧长参数化，用起来非常方便，但不是所有曲线都能成功解析转化。

二维参数化圆

以 $(x_c,y_c)$ 为圆心， $r$ 为半径的圆的参数表示可以写成：

\[\left[\begin{matrix} x \\ y \end{matrix} \right] = \left[\begin{matrix} x_c+r\cos\phi \\ y_c+r\sin\phi \end{matrix} \right]\]

为了保证曲线上的每一个点都有一个唯一确定的参数 $\phi$ ，我们可以将 $phi$ 的定义域限制为 $\phi \in [0,2\pi)$ 或者是 $\phi \in (-\pi,\pi]$ ，或其他的范围是 $2\pi$ 的半开区间。

相似的，轴对齐的椭圆的参数化形式可以表示为：

\[\left[\begin{matrix} x \\ y \end{matrix} \right] = \left[\begin{matrix} x_c+a\cos\phi \\ y_c+b \sin\phi \end{matrix} \right]\]

2.5.7 三维参数化曲线

三维参数化曲线就和二维的参数化曲线很像：

\[x=f(t)\] \[y=g(t)\] \[z=h(t)\]

比如，绕着$z$轴的螺旋线（弹簧线）可以写成：

\[x=\cos t\] \[y=\sin t\] \[z= t\]

类比二维曲线，如果我们想要控制曲线的开始和结束点，函数 $f$, $g$, $h$都应定义域为 $D \in \mathbb{R}$ 。所以可以写出它的向量形式：

\[\left[\begin{matrix} x \\ y \\ z \end{matrix} \right] = {\mathbf{p}}(t)\]

这章我们只详细讨论三维参数直线。更为广泛的三维参数曲线将在 15 章讨论。

三维参数化直线

三维参数化直线可以直接看作二维参数化直线补充一个维度，如：

\[x=2+ 7t\] \[y=1+2t\] \[z=3-5t\]

这看起来又臭又长，而且不能转化成代码，我们换向量方法描述：

\[{\mathbf{p}} = {\mathbf{o}}+t{\mathbf{d}}\]

我们取 ${\mathbf{o}}=(2,1,3)$ , ${\mathbf{d}}=(7,2,-5)$ 作为例子。

其实这和二维的情况非常相似，几何上，我前面只需要想象这条线穿过 ${\mathbf{o}}$ 并和 ${\mathbf{d}}$ 平行。对于任何 $t$ ，都会在线上得到一个点 ${\mathbf{p}}(t)$ 。比如当 $t=2$ 时，运算结果是 $(16,5,-7)$ 。主要思想是和二维一致的。

和二维一样，一条线段则可以表示为 $t \in [t_a,t_b]$ 的这样一个区间，这样，两点之间的线段就可以通过 ${\mathbf{p}}(t)={\mathbf{a}}+t({\mathbf{b}}-{\mathbf{a}})$来表示，此时 $t \in [0,1]$ ，类比可得， ${\mathbf{p}}(0) = {\mathbf{a}}$ , ${\mathbf{p}}(1) = {\mathbf{b}}$ 。

射线是具有半开区间的三维参数化直线。区间一般为： $[0,+ \infty)$ 。从此处开始，我们会将所有的直线、射线、线段统称为“光线”。虽然不太严谨，但考虑到本书的用途，以及为了让表述更简单，将做这样的规定。

2.5.8 三维参数化曲面

参数化的方法让我们很好的定义了三维空间的曲线，同样这种方法也可用于直线。但曲面的二位区域需要两个参数来描述，所以曲面写成了这样的形式：

\(x=f(u,v),\) \(y=g(u,v),\) \(z=h(u,v),\)

向量形式为：

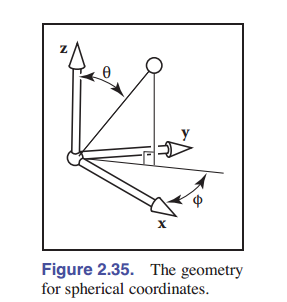
\[\left[\begin{matrix} x \\ y\\ z \end{matrix} \right] = {\mathbf{p}}(u,v)\]

举例：详见高数书本 / 考研数学 参数坐标系 中的 球坐标系。形式为：

\[x=r\cos\phi\sin\theta,\] \[y=r\sin\phi\sin\theta, \tag{2.24}\] \[z=r\cos\theta,\]

但按照我们的想法来说，我们希望它能通过向量表示。实际上这种表示方法不行。 对于给定的 $x$ , $y$ , $z$ ，我们希望能算出 $\phi$ 和 $\theta$ ，实际上通过特定函数可以算出来：

\[\theta = {\rm acos} (\frac{z}{\sqrt{x^2+y^2+z^2}})\] \[\phi = {\rm atan2} (y,x)\]

译者注：由于 arctan 函数的特性，只会返回一个 $[-\frac{\pi}{2},\frac{\pi}{2}]$ 的值，也就是只存在一四象限的返回值，我们通常使用 atan2 函数。

atan2 函数接收两个值 $\mathtt{double \ (x,y)}$，用来描述已知点的坐标，角度返回值是该点射线与 $x$ 的夹角。如 $(1，1)$ 的返回值是 $\frac{\pi}{4}$，而 $(-1,-1)$ 的返回值则是 $-\frac{3\pi}{4}$ .

对于隐式曲面，函数 $f$的导数给出了曲面的法线。而通过对曲面的参数化，对 $\mathbf{p}$ 的导数提供了该表面的几何信息。

图 2-35

考虑函数 ${\mathbf{q}}(t)={\mathbf{p}}(t,v_0)$ ，该函数定义了一条 $u$ 为常数 $v_0$ 的参数曲线。这样的线叫曲面上的 等参数曲线，简称 等参线。 $\mathbf{q}$ 的导数给出了曲线的切向量，由于曲线是在曲面上的，所以该切向量也是在曲面上的。由于上面我们将参数 $u$ 看成了一个常数，所以对 $\mathbf{p}$ 求导实际上就是对 $u$ 取偏导。将其记为 $\mathbf{p}_u$ 。类似的，另外一个偏导 $\mathbf{p}_v$ 给出了等参曲线在 $u$ 为常数的时候的切线，也就是曲面的第二条切向量。

由于我们已经得到了两条不同的切向量，可以通过向量叉乘来得出曲面的法线。法线指向的方向可以由右手法则确定。公式为： \(\mathbf{n} = \mathbf{p}_u \times \mathbf{p}_v\)

我们使用指向曲面外部的法向量。

2.5.9 曲线和曲面的总结

隐式的二维曲线 / 三维曲面由 两个/三个 标量值函数确定： $f:\mathbb{R}^2\to\mathbb{R}$ 或 $f:\mathbb{R}^3\to\mathbb{R}$ ，而曲线/面由函数值为 0 的所有点组成： \(S = \{ {\mathbf{p}}|f(\mathbf{p}) = 0 \}.\)

对于隐式曲线和隐式曲面，法向量由 $f$ 的导数（梯度）给出。然后，曲线的切向量 / 曲面的多个切向量 可以通过构造基向量从法向量导出。

对于参数化的曲线和曲面， $\mathbf{p}$ 的导数可以给出 曲线的切向量 / 曲面的多个切向量。，通过他们来构造基向量，可以导出法向量。

2.6 线性插值

图形运算中最常用的数学运算可能就是 线性插值。其实，我们在之前已经看到了一个插值的例子，就是在二维和三维中构造线段。 两个点 $\mathbf{a}$ 、 $\mathbf{b}$ 与参数 $t$ 关联，产生线 ${\mathbf{p}} = {(1-t)\mathbf{a}}+t({\mathbf{b}})$ 。这叫 插值 的原因在于 $\mathbf{p}$ 在 $t=0$ 和 $t=1$ 的时候刚好通过 $\mathbf{a}$ 和 $\mathbf{b}$ 两个点。这是 线性 的原因在于加权项 $t$ 和 $(1-t)$ 是关于 $t$ 的线性多项式。

另外一个常用的线性插值是：在一组 $x$ 轴的值 $x_1,x_2,…,x_n$ 中，对每个 $x_i$ 都有相应的 $y_i$ 与之对应，我们想要创造一个函数 $f(x)$，能让他对这些位置进行拟合，这样 $f$ 能经过每一个坐标 $(x_i,y_i)$ 。而对于线性插值，我们很自然的就可以用参数方程来解决。参数 $t$ 用于表示 $x_i$ 和 $x_{i+1}$ 之间的比例：

\[f(x) = y_i+ \frac{x-x_1}{x_{i+1}-x_i}(y_{i+1}-y_i)\]

由于加权函数是关于 $x$ 的线性函数，所以叫做线性插值。

上面两个例子都是线性插值的一般形式。

2.7 三角形

二维和三维空间内的三角形都是很多图形程序中的基本初始模型。一般来说，颜色之类的信息会标记在三角形的顶点上，然后这些信息在整个三角形上进行插值。让这样的插值变得清晰易懂的坐标系叫做 重心坐标 。我们会从头开始开发这些工具。同时，我们会在这节讨论二维三角形和三维三角形，在学习渲染屏幕上的二维图像之前，必须先学习这些。

2.7.1 二维三角形

如果我们有一个由二维坐标 $\mathbf{a}$ 、 $\mathbf{b}$ 、 $\mathbf{c}$ 定义的二维三角形，我们首先可以通过行列式确定它的面积：

\[S_{\Delta} = \frac{1}{2} \left|\begin{matrix} x_b-x_a & x_c-x_a\\ y_b-y_a & y_c-y_a \end{matrix} \right| = \frac{1}{2}(x_ay_b+ x_by_c + x_cy_a − x_ay_c − x_by_a − x_cy_b)\]

该公式会在 5.3 节推导。如果点 $\mathbf{a}$ 、 $\mathbf{b}$ 、 $\mathbf{c}$ 由顺时针表示，那么面积就是正的，否则求出来的面积会有一个负号。

图 2-36\

在图形学中，我们通常会希望一个属性（如颜色），从三角形的每个顶点平滑的进行插值过渡。有好多种方法可以做到，但最简单的是使用重心坐标。我们可以将重心坐标简单的看作一个非正交坐标系（引 2.4.2 节）。这样的坐标如图 2.36 所示。其中坐标系原点为 $\mathbf{a}$ , 基向量是 $\mathbf{b}-\mathbf{a}$ 、 $\mathbf{c}-\mathbf{a}$ 。

这样，所有的点 $\mathbf{p}$ 都可以写成:

\[\mathbf{p}=\mathbf{a}+\beta(\mathbf{b}-\mathbf{a})+\gamma(\mathbf{c}-\mathbf{a})\]

然后整理此式，得到：

\(\mathbf{p} = (1-\beta-\gamma)\mathbf{a}+\beta\mathbf{b}+\gamma\mathbf{c}\) 然后我们通常为了简洁，新定义一个 $\alpha$ ：

\[\alpha \equiv 1-\beta-\gamma\]

这样就会有下面简洁的式子： \(\mathbf{p}(\alpha,\beta,\gamma) = \alpha\mathbf{a}+\beta\mathbf{b}+\gamma \mathbf{c},\)

\[\alpha+\beta+\gamma = 1.\]

我们刚开始看到重心坐标的时候，感觉重心坐标像是一个抽象、不太直观的构造，但后面我们就会发现，重心坐标很强大、很方便。这就像在一个有两组平行街道（但相互不成直角）的城市里，你会发现街道地址很有用。自然中的系统本身就是一种重心坐标，你会很快习惯它。重心坐标可以定义平面上的所有点。重心坐标一个很好用的特性就是它可以方便的判断一个点 $\mathbf{p}$ 是否在点 $\mathbf{a}$ 、 $\mathbf{b}$ 、 $\mathbf{c}$ 组成的三角形内部。若在内部，则一定有下面的式子，反之亦然：

\[0<\alpha<1\] \[0<\beta<1\] \[0<\gamma<1\]

同样的，如果 $\alpha$ 、 $\beta$ 、 $\gamma$ 中有两个 0，另外一个是 1，那么说明你在顶点上；如果有一个 0，两个在 $(0,1)$ 内，说明这个点在三角形的边上。另外一个很好的特性是重心坐标使用了上面那个加权方程，它能平滑的混合三个顶点的坐标，而这样的三个系数 $\alpha$ 、 $\beta$ 、 $\gamma$ 同样可以用来对颜色等属性进行平滑插值。我们在下一章就能见到了。

给定一个点 $\mathbf{p}$ ，我们如何计算它的重心坐标呢？一种方法是像上面所说的那样，写出 $\mathbf{p}$ 由 $\mathbf{a}$ 、 $\mathbf{b}$ 、 $\mathbf{c}$ 表示的式子，然后替换得到 $\alpha$ 、$\beta$ 、 $\gamma$ 。我们可以通过线性代数的方式写出公式：

\[\left[\begin{matrix} x_b-x_a & x_c-x_a \\ y_b-y_a & y_c-y_a \end{matrix} \right]\left[\begin{matrix} \beta \\ \gamma \end{matrix} \right] = \left[\begin{matrix} x_p-x_a \\ y_p-y_a \end{matrix} \right]\]

虽然可以很简单的计算出代数结果，但是计算一个几何解是大有裨益的：

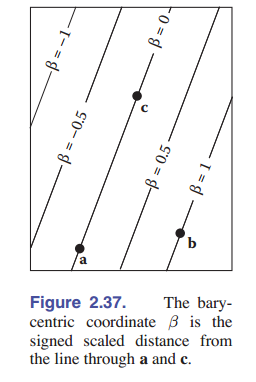
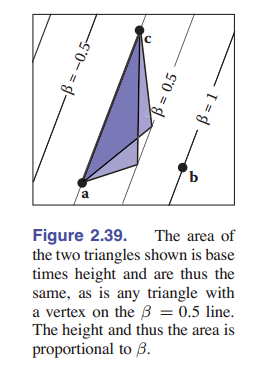
重心坐标的一个几何特性是，它们代表了直线到三角形一侧的带符号的缩放间隔。如 [图 2-37] 中的 $\beta$ 。我们回想一下 [2.5.2 节]（二维梯度）中的距离计算，可知将 $x,y$ 代入方程 $f(x,y)$ 可以获得点 $(x,y)$ 和直线 $f(x,y) = 0$ 之间的带符号缩放距离。同时，等式两边同乘一个非零 $k$ ，直线还是那条直线，但是改变了 k，距离的大小和正负也随之进行倍数变化。下面举个例子：$kf(x,y)=\beta$。如上图，由于只有 $\mathbf{b}$ 不在三角形上，所以 $\beta=1$ ,抑或是我们只知道直线穿过了 $\mathbf{a}$ 点和 $\mathbf{c}$ 点，那么可以通过计算得出 $\beta$ :

\[\beta = \frac{f_{ac}(x,y)}{f_{ac}(x_b,y_b)}\]

同样的，我们可以用这个方法计算出 $\alpha$ 和 $\gamma$ 。为了方便，由于三者加起来是 1，我们只需要计算出两个参数即可。

图 2-37 图 2-38

为了通过 $\mathbf{p}_0$ 和 $\mathbf{p}_1$ 找到这条线的理想形式，我们用 2.5.2 节（二维梯度）学习的知识来找出一些有帮助的隐式直线：通过两点写出一般式：

\[f_{ab} \equiv (y_a-y_b)x+(x_b-x_a)y+x_ay_b-x_by_a=0\]

由于 $f_{ab}(x_c,y_c)$ 是不为 1 的，所以它还能继续优化。两边同除，我们得到：

\[\gamma = \frac{(y_a-y_b)x+(x_b-x_a)y+x_ay_b-x_by_a}{(y_a-y_b)x_c+(x_b-x_a)y_c+x_ay_b-x_by_a}\]

除法的存在会让人担心除零错，但是由于面积不为 0 或者不接近于 0 的三角形，我们不需要担心。同理可得 $\beta$ 的值，然后相减即可：

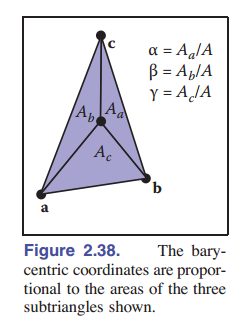
\[\beta = \frac{(y_a-y_b)x+(x_b-x_a)y+x_ay_b-x_by_a}{(y_a-y_b)x_b+(x_b-x_a)y_b+x_ay_b-x_by_a}\] \[\alpha = 1-\beta\gamma\]

其实还有另外一种方法计算重心坐标：如图 2.38 所示，我们可以计算小三角形 $A_1$、 $A_2$ 、$A_3$ 的面积，然后重心坐标遵循下面的规则，规范化重心坐标等于面积比值：

\[\alpha = \frac{A_a}{A}\] \[\beta = \frac{A_b}{A}\] \[\gamma = \frac{A_c}{A}\]

请注意，如果点在外面，计算出的三角形面积应该是负数。只要计算出正确的带符号面积，然后进行比值，就是正确的重心坐标结果。

图 2-39 图 2-40

2.7.2 三维三角形

重心坐标让我们从二维到三维的转换变的如此自然。

假设三维空间内的三角形由 $\mathbf{a}$ 、 $\mathbf{b}$ 、 $\mathbf{c}$ 三个点组成，我们还是可以使用之前的表达式：

\[\mathbf{p} = (1-\beta-\gamma)\mathbf{a}+\beta\mathbf{b}+\gamma\mathbf{c}\]

然后，当我们改变 $\beta$ 和 $\gamma$ 的时候，三角形会扫出一片平面。

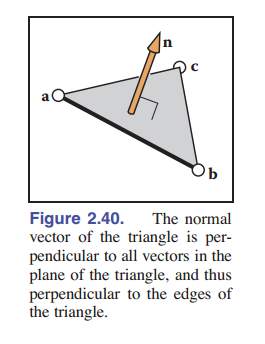
三角形的法向量很简单，只需随便找到两个边向量进行叉乘即可：

\(\mathbf{n} = (\mathbf{b}-\mathbf{a})\times(\mathbf{c}-\mathbf{a}) \tag{2.34}\) 请注意，该法向量算出来不是单位向量，同时符合使用的两个向量的右手定则。

叉乘同时具有几何意义：三角形面积是两条边向量叉乘结果的一半：

\[S_\Delta =\frac{1}{2}\parallel (\mathbf{b}-\mathbf{a})\times(\mathbf{c}-\mathbf{a})\parallel \tag{2.35}\]

由于这 不是带符号面积 ，所以不能直接用于计算重心坐标。但是！我们可以观察这个三角形：我们以顺时针方向看得出的法向量和逆时针的法向量是符号相反的。

让我们回想以下向量的点乘：

\[\mathbf{a} \cdot \mathbf{b} = \parallel\mathbf{a}\parallel \ \parallel\mathbf{b}\parallel\cos\phi,\]

其中 $\phi$ 是两个向量之间的夹角。当向量 $\mathbf{a}$ 和 $\mathbf{b}$ 平行时， $\cos \phi=\pm1$ ，这让我们有办法判断向量是否同向/反向。

所以，这样做即可算出重心坐标：

首先，构造不同的法向向量 $\mathbf{n}_a$ 、 $\mathbf{n}_b$ 、 $\mathbf{n}_c$ 。如 $\mathbf{n}_a$ ，是由顶点 $\mathbf{b}$ 、 $\mathbf{c}$ 、 $\mathbf{p}$ 经过上面的求法向量叉乘方程计算得出的。具体如下：

\[\mathbf{n}_a = (\mathbf{c}-\mathbf{b})\times(\mathbf{p}-\mathbf{b})\] \[\mathbf{n}_b = (\mathbf{a}-\mathbf{c})\times(\mathbf{p}-\mathbf{c})\] \[\mathbf{n}_c = (\mathbf{b}-\mathbf{a})\times(\mathbf{p}-\mathbf{a})\]

然后通过求 $\cos \phi$ 的方式求出 $\alpha$, $\beta$, $\gamma$：

\[\alpha = \frac{\mathbf{n}\cdot\mathbf{n}_a}{\parallel\mathbf{n}\parallel^2}\] \[\beta = \frac{\mathbf{n}\cdot\mathbf{n}_b}{\parallel\mathbf{n}\parallel^2}\] \[\gamma = \frac{\mathbf{n}\cdot\mathbf{n}_c}{\parallel\mathbf{n}\parallel^2}\]

即可算出重心坐标。

常见问题

第三章 光栅图像

大部分计算机图形图像以某种光栅显示方式呈现给用户。光栅显示将图片以像素组成的矩形阵列显示出来。

像素（pixel） 是图片元素（picture element）的缩写。

一个常见的例子就是平板电脑显示器或电视，他们有一个由小型发光像素组成的矩形阵列，可以独立的设置颜色，显示任意的图像。不同的颜色通过混合红、绿、蓝三种颜色产生。其实，大部分打印机，如激光打印机和喷墨打印机，也可以算是光栅设备，因为他们是基于扫描的。虽然像素之间没有实际上的分隔，但是图像是通过在虚拟的网格中顺序的点上墨水形成的。

光栅在图像输入设备中也非常的普遍。数码相机有一个图像传感器，图像传感器是由一组感光像素网格组成，每个感光像素都能感受落在它上面的光的颜色和亮度。桌面扫描仪包含了一个线性的像素阵列，它可以扫过需要扫描的页面，每秒运行多次来生成一组像素网格。

但我们不想通过这种方法来显示图像。我们可能会需要改变图像的大小、方向、校正颜色，抑或是显示移动的三维空间中的投影图像。就算是电视，显示器的像素和显示的图像的像素也不是相同的。基于上面这些情况考虑，图片像素和显示像素并不能直接联系起来。我们最好将光栅图像视为一种与设备独立的图像的描述，而将显示设备的功能看作模拟显示目标图片的大致信息。

除了使用像素阵列，还有一种方法可以描述图像：矢量图。矢量图不参考像素网格，而是存储形状信息（直线或曲线包裹的颜色）来描述图像。从本质上说，这其实是存储了如何显示图像的指令，而不是显示图像的像素。矢量图的主要优点在于它和分辨率无关，可以在非常高分辨率的显示器上显示。矢量图一般用于文本、图标、工业制图，以及其他对精度要求高，但对图像计算和复杂阴影不怎么需要的应用场景。

这一章，我们会讨论光栅图像和显示的基础知识，同时特别关注标准显示的非线性。当我们在之后的章节讨论计算图像时，我们必须留意像素值和光照强度是如何联系在一起的。

3.1 光栅设备

在抽象地讨论光栅图像之前，先看看使用光栅图像的设备吧家人们。一些常见的光栅设备可以简单的分为以下结构：

3.1.1 显示技术

现在的显示器，包括电视和数字电影放映机，以及电脑的显示器，都是基于固定像素阵列的。他们可以分为自发光型和透光型显示器。自发光型显示器使用直接能够发射光线的不同颜色的光源制成，而透光型显示器需要在透光板后面有一个白色光源（显示器背光/投影仪光源），然后透光板可以改变透光的光量和颜色。

发光二极管（LED）显示屏是一种自发光型显示器的代表。每个像素都由一个或多个 LED 组成。LED 是基于有机/无机半导体的一种材料，它发光的强度取决于当前流过的电流大小。

彩色 LED 显示器的一个像素可以分为三个 子像素 ：每个子像素由不同的材料构成，可以单独控制。人眼在远距离无法准确分辨三种子像素，所以它们组成的光是最后的显示效果。

液晶显示器（LCDs）是透光型显示器的代表。液晶是一种分子结构可以旋转的材料。它可以通过电压控制旋转，旋转后能改变它的透光性。一个液晶像素（图 3.3）的后面有一层偏振片，它会被偏振光照亮（在水平偏振光的条件下）。

图 3-3

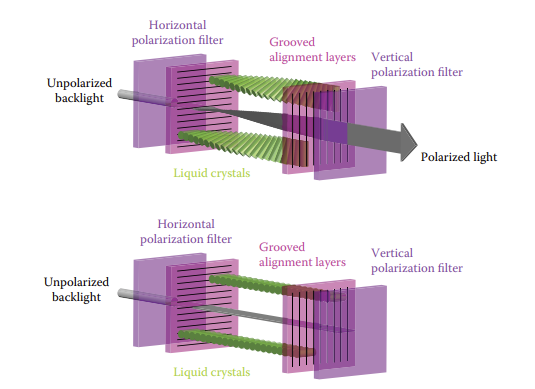
偏振片的第二层偏振膜被定向为只传输垂直偏振光。如果电压设置为不改变偏振方向，那么光线会被一二层的偏振膜完全阻挡，也就是像素呈“关闭”状态。同样的，如果电压让二层偏振膜旋转了 90°，那么所有水平光都不会被阻挡，也就是“开启”状态，这时光强将达到最大。而中间值的电压会让液晶翻转一部分，这样就会部分透光。和 LED 显示器一样，彩色液晶的每个像素也可以分为红蓝绿三个子像素。

任何具有固定像素网格的显示器，（包括上面的显示技术，或是其他技术）都会有一个基于屏幕网格的固定分辨率。对于显示器和图像，分辨率 的意思就是像素网格的尺寸：如果一个桌面显示器有 1920x1200 的分辨率，那么它就一共有 2,304,000 个像素，横向有 1200 个行，纵向有 1920 个列。

而对于要显示的东西必须以 1920x1200 的分辨率填满整个屏幕，我们会使用第九章的方法来完成这一步骤。

3.1.2 硬拷贝设备

在纸上永久记录图像有很严的限制，和在屏幕上显示图像完全不一样。在印刷中，颜料分布在纸或者其他介质中，然后光照到它，反射不一样颜色的光，你才能产生图像。打印机是类似于图像的光栅设备，但很多打印机只打印二进制图像，也就是要么没有墨水，要么有墨水，没有中间值（灰度）的选项。

喷墨打印机就是通过扫描来形成光栅图像的一个示例。一个喷墨打印机携带着可以化成小液滴喷在纸上的液态墨水。空白的地方当然就不喷墨水了。彩色打印就是使用多个不同颜色墨水组合而成的。很多喷墨打印机会有多个喷头，但决定行间距的并不是喷头，而是纸张行动的距离。

热转移印花 是进行连续色调打印的一个例子，这意味着可以在纸上打印不同量的染料，而不是像喷墨打印机那样要么有要么没有。

图 3-6

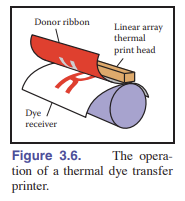
包含彩色染料的供体色带 被压在纸和染料接收器之间，然后一个带有加热元件的打印头会控制是否加热每一排中的像素。每一种颜色的染料都会重复这个过程一遍。可以通过温度的高低控制染料的转移程度，从而产生连续范围的颜色。打印头的提供了整个页面横向上的像素，但页面竖向上的像素由加热冷却速度与纸张速度之比决定。

和显示器不同，打印机的分辨率更多的使用 像素密度 进行描述。所以一个热转移打印机如果在 1 英寸的空间里有可以打印 300 个像素的打印头，那么我们可以简单的说这台打印机的分辨率是 300ppi。而一个每英寸内具有 1200 个网格的喷墨打印机，我们称它的分辨率是 1200dpi。因为喷墨打印机是二进制设备，它需要更高的打印分辨率来保证打印质量，这出于两个原因：一是由于打印边界是黑白边界，需要高分辨率来防止发生阶梯状步进、走样（见 8.3 节）。二是当用二进制来模拟打印连续色调图像时，也需要通过改变打印密度来调整颜色，这称作半色调。

注：dpi 现在广泛用于描述“每英寸像素”，但实际上应该使用 ppi 描述，而 dpi 原来指的是专用于描述二进制设备的分辨率。

3.1.3 输入设备

光栅图像不是凭空生成的，而除了算法生成的图像外，任何图像都需要由 光栅输入设备 来捕捉。最常见的有照相机和扫描仪。就算是在渲染三维场景的时候，照片也常常用来做纹理贴图（见 11 章）。一个光栅输入设备必须能够测量每个像素的光线，所以通常是由传感器阵列组成的。

数码相机是二维阵列输入设备的代表。照相机里的图像传感器是一个由光敏像素网格构成的半导体。由两种常用类型：电荷耦合器件（CCDs）和互补金属氧化物半导体（CMOS）。照相机的镜头将要拍摄的物体映到传感器上，然后传感器的每个像素会测量落在上面的光强度，最终产生数据，构成输出图像。就像显示器由三种颜色的子像素构成一样，大部分彩色相机使用 滤色器阵列 或 马赛克 来让每个像素只能接收红、绿、蓝光，然后让图像处理软件填充缺失值（称为 去马赛克 ）。如图 3.8：

图 3-8

其他相机使用三个独立的阵列或三个独立层来测量每个像素上独立的红、绿、蓝三种颜色，然后就能生成不需要进一步处理的可用图像。照相机的分辨率由阵列中的像素数量决定，通常用像素总量来描述：如果一个相机有 3000x2000 的像素阵列，就称作 6 百万像素（MP）照相机。要注意马赛克传感器的每个像素不能完整的记录所有的颜色信息，所以分辨率相同的情况下，采用独立像素的相机记录的图像信息更多。

平板扫描仪也于每一格像素单独测量红、绿、蓝的颜色值，但它类似于热转移打印机，只有一维阵列，通过一维阵列扫过需要扫描的页面，每秒进行多次扫描。横方向的分辨率由阵列所确定，所以是固定的，而纵方向的分辨率则由测量频率和移动速度之比决定。一个彩色扫描仪有一个 $3\times n_x$ 的像素序列，其中 $n_x$ 是整个页面的像素总数， $3$ 则是由三行红、绿、蓝过滤器组成。通过测量三种颜色之间加入适当的延迟时间，可以做到对每一个点都进行三次不同颜色的测量。和连续色调打印机类似，扫描仪的分辨率由 ppi 表示。

扫描仪的分辨率有些时候称作 光学分辨率 ，因为大部分扫描仪可以通过内置的转换装置输出不同分辨率的图像。

有了这些神奇知识，接下来我们就能更详细、更抽象地探讨图像了，然后我们就可以使用图像算法来调理它了。

3.2 图像、像素和几何

我们知道，光栅图像时一个像素的巨大阵列，每一个像素都存储着在那一个网格里的颜色信息。我们已经了解了输出设备处理我们发给它的图像的过程，也了解了输入设备从自然世界的光线中获取图像的过程。但在计算机中，我们需要提取出一个与这些设备都不一样的抽象方法，用它来推理产生或转换存储在图像里的数值的方法。

当我们测量/再现图像的时候，它接收二维的光分布形式的数据：显示器发出的光是显示器表面位置的函数；落在相机传感器上的光是传感器平面上位置的函数；反射比，也就是反射回来光的比例（与吸收比相反），是关于一张纸上位置的函数。所以在现实世界中，图像就是定义在二维区域（绝大部分是矩形）上的函数。所以我们可以将图像抽象成一个函数： \(I(x,y):R\rightarrow V,\) 这里面 $R\subset \mathbb{R}^2$ ，是一个矩形区域， $V$ 是一组像素点的集合。最简单的例子是理想化的灰度图像，矩形像素区域的每个点都只有一个亮度，但没有颜色，那么我们就可以说 $V=\mathbb{R}^+$ （也就是非负实数）。同样的，一个理想化的彩色图像，有 $V=(\mathbb{R}^+)^3$ 。我们将会在下一节着重讲解 $V$ 的取值问题。

请注意，像素指的不是一个小方块，而是一个点！

那么光栅图像和连续图像，他们的抽象概念又有什么关联呢？让我们康康具体的例子：来自相机/扫描仪的单个像素，其实是测量了该像素对应的那块图像表面颜色的平均值。而一个显示用的像素（包括红、绿、蓝子像素）是这样设计的：该像素表面的平均颜色由对应的光栅图像中的像素值控制。上面两个例子里，像素值都是图像局部颜色的平均值，称为图像的 点样本 。换句话说，当我们拥有像素的值 $x$ 时，说明“在这个网格周围的像素值是 $x$ ”。这种思想称为图像作为函数的采样。我们将在第 9 章探讨这个问题。

有一个普信问题：像素在二维空间里的位置如何表示？ 这其实只取决于个人的使用习惯，但是，建立一个一致的惯例非常重要！这本书里，我们将光栅图像的像素建立成 $(i,j)$ 这样的坐标形式，从左下角开始计数。如果图像有 $n_x$ 列和 $n_y$ 行像素，那么最左下角像素就是 $(0,0)$ ，最右上角则是 $(n_x-1,n_y-1)$。我们需要一个二维的真实屏幕坐标来表示像素的位置。我们将像素采样点放在整数坐标上，就像下图 3.10 中，有一个 $4\times3$ 的坐标面。

图 3-10

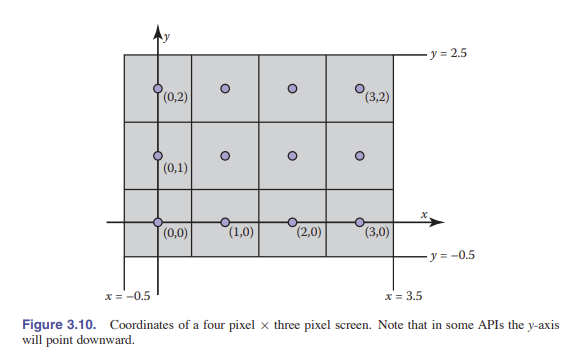
上图的矩形域宽度是 $n_x$ ，长度是 $n_y$ ，同时像素是以整数坐标作为中心的，这就说明它在采样点之外还会有半个像素超出坐标轴。所以具体的矩形域是： \(R=[-0.5,n_x-0.5]\times[-0.5,n_y-0.5]\)

再次说明，我们只是约定了这样的表达形式，但是以后实现摄像机和视图转换的时候，记住他们是很重要的。

3.2.1 像素值

至此为止，我们已经使用实数来描述了像素值，来代表图像中某一点的强度（可能分成三块，红、绿、蓝）。这说明图像应该是浮点数组成的阵列，每个点拥有一个（灰度图像）或者三个（彩色图像）32 位浮点值。在需要精度和范围的时候，有时我们会使用这种格式。但同时，图像有很多个像素，需要很多内存和带宽，通常情况下提供不了这么多。一张 1000 万像素的图片通过这种方法存储就要占据约 115MB 的内存。

问：为什么是 115MB 而不是 120MB？ 答：(((10000000×3×32)÷1024)÷1024)÷8=114.44MB

对于直接显示的图像，需要记录的光强范围就更小。虽然现实世界里光强度没有上限，但任何设备都有一个最大光强的限度。一般为了简单，范围使用 $[0,1]$ 。比如，对于一个 8-bit 图像，光强度可能的值有 $0,1/255,2/255,…,254/255,1.$ 使用浮点数存储的图像允许使用更大范围的值，通常与固定范围/低动态范围（ LDR ）分开比较，称为高动态范围（ HDR ）。在 21 章我们会深入讨论关于 HDR 图像的技术与应用。

下面是一些典型应用程序中的像素格式：

减少用于存储每个像素信息的比特位会导致两种不同种类的 伪影，或产生人工引入的照片瑕疵。首先，如果像素值比能显示的最大亮度还要亮，就会产生“裁剪效应”。比如，一张大太阳的照片，会有一些地方的太阳光反射比白色表面还要亮，但超出了显示范围（就算相机能捕捉到更大的信号），转化成固定范围照片也会产生裁剪效应，显示不出来。第二，编码精度有限的图像，在将像素进行四舍五入到最近精确值时，会产生 量化噪声 或 色带。在动画或视频中，视频变化不大的时候，色带可能不易察觉，但当画面来回移动时，色带会变得非常明显，影响观感。

此处的色带和上提及的色带不是一个东西，此处指色彩条带。也就是低分辨率视频上出现的一坨奇怪的颜色。

3.2.2 显示器的显示强度 和 Gamma 值

所有的现代显示器都接收数字输入的像素“值”，转化成显示的强度。真实情况下，显示器通电但关闭的情况下仍然会反射一些光出来。为了方便，我们将关闭的显示器视为黑色，完全打开的显示器视为白色，假设黑色是 0，白色是 1，白色和黑色中间的灰是 0.5。

此 0.5 指来自像素的物理光强，而不是外观，因为人类对光线的感知不是线性的，我们将在 20 章展开说说。

要在显示器上显示正确的图像，有两个关键问题必须明白：第一个是，显示器对输入做出的反应是非线性的，比如假设你给了显示器三个像素分别是 0，0.5，1 的值，但显示器显示的三个像素光强可能是 0，0.25，1。这种非线性的近似表征，我们一般通过 Gamma 值（ $\gamma$ ）来表述。 $\gamma$ 值表示公式中的自由度：

\[\rm displayed \ itensity=(maximum \ intensity)a^\gamma\]

其中 a 是在 0 到 1 之间的输入像素值。举个例子，假设一个显示器有 2.0 的 $\gamma$ 值，然后我们输入的 a 是 0.5，那么显示器的显示强度则是最大强度的 $\frac{1}{4}$ . 同时需要注意的是，如果 a 是 0 或 1，那么不管你输入的 $\gamma$ 值是多少，最终的强度都是最小强度/最大强度。使用 $\gamma$ 值来衡量显示器非线性只是一个近似值；但我们并不需要很准确的测量一个设备的 $\gamma$ 值。衡量非线性的一个很好的办法是：寻找在什么样的 a 的条件下，亮度值会在 0.5，即如下：

\[0.5 = a^\gamma\]

如果我们能得到 a 的值，那么 $\gamma$ 值也能推导出来。而 a 是可以通过一些手段得到的：我们可以通过显示一个只有黑白像素的棋盘图案，右边放一个随 a 改变灰度的灰色图像，然后要求观察者调整 a（比如用滑块调整之类）：当你离远了看，两者区分不出来的时候就能得到 a 的值，然后通过 $\gamma = \frac{\ln0.5}{\ln a}$ 来算出 $\gamma$ 值。

当我们知道了 $\gamma$ 值之后，就可以进行Gamma 校正，让该公式里的 a 为 0.5 的时候屏幕也显示 0.5 的光照强度，采用以下的公式完成： \(a' = a^{\frac{1}{\gamma}}\) 将这个公式代回，我们就能得到：

\[\rm displayed \ indensity = (a')^\gamma = (a^\frac{1}{\gamma})^\gamma = a \ (maximum \ intensity)\]

真实世界里显示器的另外一个特性就是它们采用量化的输入值。因此虽然我们可以任意修改值为 $[0,1]$ 内的浮点数，但显示器的输入会将其转化并舍入为固定大小的整数。最常见的是 8 位存储，会被转化为 0-255 之间的整数。这就说明了 a 的可能值就已经不是所有 $[0,1]$ 里面的小数，而是 ${\frac{0}{255},\frac{1}{255},\frac{2}{255},…\frac{254}{255},\frac{255}{255}}.$

那么显示器的最大光强值就大约是 ${M(\frac{0}{255})^\gamma,M(\frac{1}{255})^\gamma,M(\frac{2}{255})^\gamma…,M(\frac{254}{255})^\gamma,M(\frac{255}{255})^\gamma}.$ , 此处M是最大光强，作为系数。在需要精确控制光强的应用场景，我们必须测量 256 种可能的强度，而且这些光强在屏幕上不同的像素点可能会不一样，尤其对于 CRT 显示器来说。它们也可能随视角而变化。幸运的是，很少有应用场景需要如此精确的校准。

3.3 RGB 色彩

大多数计算机图形的图像是在 RGB 色彩里定义的。RGB 色彩空间是一个可以让计算机屏幕直接转换控制信息的工具。在这一节中，我们将从用户的角度探讨 RGB 色彩，目标是能够顺利使用它们。对于颜色，更透彻的讲解会在第 19 章，但 RGB 颜色空间的机制已经能让我们编写绝大部分图形程序了。RGB 色彩空间的基本思想就是混合三种基色，红、绿、蓝，来组成各种颜色。三种基色以叠加的方式经常处理。

在 RGB 中叠加色彩，我们有图 3.12 上所示的的结果：

如果我们能将基色光的强度进行调整，让它从全关（即像素值 0）慢慢调整到全开（即像素值 1），我们就能调出 RGB 显示器上能显示的所有颜色。我们可以将红、绿、蓝三种像素创建一个RGB 立方体，图 3.13 展示了立方体的样子。立方体的各个角的坐标是：

图 3-13

\(黑色 = (0,0,0)\) \(红色 = (1,0,0)\) \(绿色 = (0,1,0)\) \(蓝色 = (0,0,1)\) \(黄色 = (1,1,0)\) \(洋红 = (1,0,1)\) \(青色 = (0,0,0)\) \(白色 = (1,1,1)\)

实际上的 RGB 级别通常是以量化形式给出的，就类似 3.2.2 节提到的灰度一样，每个灰度级别都使用一个整数来表示，这些整数常用的是一个字节，也就是 8 位，所以每个 RGB 分量由 0-255 之间的整数组成，三个整数加起来占用 24 位的空间。所以一个具有“24 位色彩”的系统，对于每个颜色分量都有 256 种级别。RGB 分量同样适用与前文所讲的 Gamma 校正 的问题。

3.4 透明度合成

通常，我们对图像进行处理的时候会只想覆盖一部分区域的像素。一个很常见的例子就是 合成图像 ，即我们有一张图做背景，想要在这章背景图的前面加上一张图。对于前景中不透明的像素，我们只需要替换掉它们即可，同样的，前景中全部透明的像素就不需要加以处理，而对于那些半透明的像素，我们就要加以小心了。前景对象有部分透明的情况有玻璃等。但是，我们遇到的最常见的前景和后景需要像素融合的情况反而不是这个，而是当前景仅覆盖单个像素的一部分时，比如前景的边界，或者前景物体有一个子像素洞，如树叶中间的孔。

将前景对象和背景对象进行混合的一个重要部分就算需要提供 像素覆盖率 。像素覆盖率能指明前景像素需要占的比例。我们将这个比率记为 $\alpha$ 。如果我们想要在背景色 ${\mathbf{c}}_b$ 上合成前景色 ${\mathbf{c}}_f$ ，比率为 $\alpha$ ，我们就可以使用公式：

\[{\mathbf{c}} = \alpha {\mathbf{c}}_f+(1-\alpha){\mathbf{c}}_b\]

我们将不透明的前景层的合成解释为，前景对象覆盖了单个像素的 $\alpha$ 部分，然后背景对象覆盖了单个像素的剩下 $(1-\alpha)$ 部分。对于一个透明的层（如玻璃上有颜料或者半透明涂料），合成的解释是前景阻挡了背景 $(1-\alpha)$ 部分的光，然后自己 $\alpha$ 部分的光来将被阻挡的光进行补全。图 3.14 提供了使用公式的例子。

简易来说，Alpha 指 “不透明度”。

图像中所有像素对应的 $\alpha$ 值可能会存储在一个单独的灰度图像中，这个图像一般称之为Alpha 蒙版 或 透明度蒙版。或者，该信息会被看作是除了 RGB 外的第四个色彩通道，称为Alpha 通道，然后这图像就可以被称作RGBA 图像，每个通道 8 位，共 32 位。 32 位的存储在大多数计算机里是一个方便存储的块（chunk）。

尽管上面的透明度公式普遍适用，但是也有一些情况下 $\alpha$ 的使用方式不同 (Porter & Duff, 1984)

注：此处指 Porter-Duff 颜色混合模式，此混合模式较为复杂，有空将会详细讨论。

3.4.1 图像存储

大多数 RGB 图像格式使用每个颜色通道 8 比特进行存储。这导致了一张原始的百万像素图像的存储大小接近 3M。为了减少存储空间，大多数图像格式允许对图像进行某种方式的 压缩。压缩方式存在 有损压缩 和 无损压缩 ，无损压缩不存在信息的丢失，但有损压缩的过程中必定会有信息在压缩后无法复现。比较流行的压缩方式有：

由于压缩和格式转化，我们需要编写不同的输入/输出例程（Routines，可理解成服务）。幸运的是，我们可以使用 库例程 来读写标准文件格式。对于那些编写速度比运行效率更重要的应用程序，一个简单的选择是使用原始 PPM 文件，这种文件可以简单的讲内存中的图像通过数组转存到文件中，然后加上一个合适的头文件，就是原始 PPM 文件了。非常的简单。

常见问题

</div>